Question

The coordinates of a particle moving in a plane are given by
x(t)= a cos (pt)and y(t)= b sin (pt) where a,b (< a)and
p are positive constants of appropriate dimensions. Then,

• A. the path of the particle is an ellipse
• B. the velocity and acceleration of the particle are normal to
  each other at t = $\pi$/2p
• C. the acceleration of the particle is always directed towards
  a focus
• D. the distance travelled by the particle in time interval t - 0 to t = $\pi$/2p is a

Answer 1

Answer: (A), (B), (C)

$x=acos(pt)\Rightarrow cos(pt)=\frac{x}{a}$ ...(i)
$y=bsin(pt)\Rightarrow sin(pt)=y/b$ ...(ii)
Squaring and adding Eqs. (i) and (ii), we get
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Therefore, path of the particle is an ellipse. Hence, option
(a) is correct.
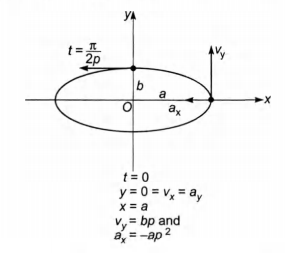
From the given equations we can find
$\frac{dx}{dt}=v_x=-apsinpt,\Rightarrow \frac{d^{2}x}{d{t}^2}=a_x=-a{p}^{2}cospt$
$\frac{dy}{dt}=v_y=bpcosptand\frac{d^{2}y}{d{t}^2}=a_y=-b{p}^{2}sinpt$
At time t$=\pi /2porpt=\pi /2$
a${}_x$ and v$-v$ become zero (because cos $\pi$/2 = 0)
only v${}_x$ and a${}_y$ are left.
or we can say that velocity is along negative x-axis and
acceleration along y-axis.
Hence, at t = $\pi$/2p velocity and acceleration of the particle
are normal to each other. So, option (b) is also correct.
At t = t, position of the particle
$r(t)=x\hat{i}+y\hat{j}=acsopt\hat{i}+bsinpt\hat{j}$
and acceleration of the particle is
$a(t)=a_x\hat{i}+a_y\hat{j}=-p^2[acospt\hat{i}+bsinpt\hat{j}]$
$=-p^2[x\hat{i}+y\hat{j}]=-p^{2}r(t)$
Therefore, acceleration of the particle is always directed
towards origin.
Hence, option (c) is also correct.
At t = 0, particle is at (a,0) and at t = $\pi$ / 2p
particle is at (0,b). Therefore, the distance covered is
one-fourth of the elliptical path not a.
Hence, option (d) is wrong.