Q.
The coordinates of a particle moving in a plane are given by
x(t)= a cos (pt)and y(t)= b sin (pt) where a,b (< a)and
p are positive constants of appropriate dimensions. Then,
IIT JEEIIT JEE 1999
Solution:
$x=a cos(pt) \, \, \Rightarrow \, \, \, cos(pt)=\frac{x}{a} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $ ...(i)
$y=bsin (pt) \, \, \, \Rightarrow \, \, \, \, sin(pt)=y/b \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $ ...(ii)
Squaring and adding Eqs. (i) and (ii), we get
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
Therefore, path of the particle is an ellipse. Hence, option
(a) is correct.
From the given equations we can find
$\frac{dx}{dt}=v_x =- ap \, sin \, pt, \, \, \Rightarrow \, \, \, \frac{d^2x}{dt^2}=a_x =-ap^2cos pt$
$\frac{dy}{dt}=v_y=bp \, cos \, pt \, and \, \, \frac{d^2y}{dt^2}=a_y=-bp^2 \, sin pt$
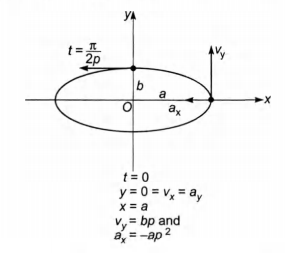
At time t$=\pi/2p \, or \, pt=\pi/2$
a$_x$ and v$-v$ become zero (because cos $\pi$/2 = 0)
only v$_x$ and a$_y$ are left.
or we can say that velocity is along negative x-axis and
acceleration along y-axis.
Hence, at t = $\pi$/2p velocity and acceleration of the particle
are normal to each other. So, option (b) is also correct.
At t = t, position of the particle
$ \, \, \, \, \, r(t)=x\widehat{i}+y\widehat{j}=a \, cso pt\widehat{i}+b \, sin pt\widehat{j}$
and acceleration of the particle is
$a(t)=a_x \widehat{i}+ a_y \widehat{j}=-p^2[a \, cos \, pt \widehat{i} +b sin \, pt \widehat{j}]$
$=-p^2[x\widehat{i}+y\widehat{j}] =-p^2 r (t)$
Therefore, acceleration of the particle is always directed
towards origin.
Hence, option (c) is also correct.
At t = 0, particle is at (a,0) and at t = $\pi$ / 2p
particle is at (0,b). Therefore, the distance covered is
one-fourth of the elliptical path not a.
Hence, option (d) is wrong.