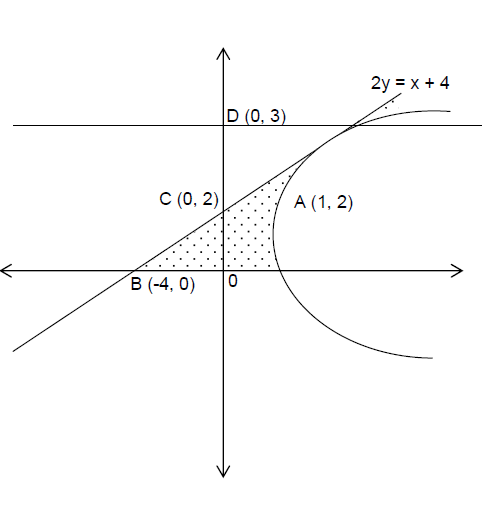
Question

The area of the region bounded by the parabola $(y-2{)}^2=x-1$ , the tangent to the parabola at the point $(2,3)$ and the $x$-axis is

• A. $3$
• B. $6$
• C. $9$
• D. $12$

Answer 1

Answer: (C)

Equation of tangent at (2, 3) to
$(y-2{)}^2=x-1$ is $S_1=0$
$\Rightarrow x-2y+4=0$
Required Area = Area of $\Delta OCB+$ Area of $OAPD-$ Area of $\Delta PCD$
$=\frac{1}{2}\left(4\times 2\right)+$ $\underset{0}{\overset{3}{\int }}(y^2-4y+5)dy-$$\frac{1}{2}\left(1\times 2\right)$
$=4+{\left[\frac{y^3}{3}-2y^2+5y\right]}_{{}_{{}_0}}^{{}^{{}^3}}-1=4-9-18+15+-1$
$=28-19=9$ sq. units
(or)
Area $=\underset{0}{\overset{3}{\int }}(2y-4-y^2+4y-5)dy-\underset{0}{\overset{3}{\int }}(y^2+6y-5)dy=-$$\underset{0}{\overset{3}{\int }}(3-y{)}^{2}dy$$={\left[\frac{{\left(y-3\right)}^3}{3}\right]}_{{}_{{}_0}}^{{}^{{}^3}}=\frac{27}{3}=9$ sq.units