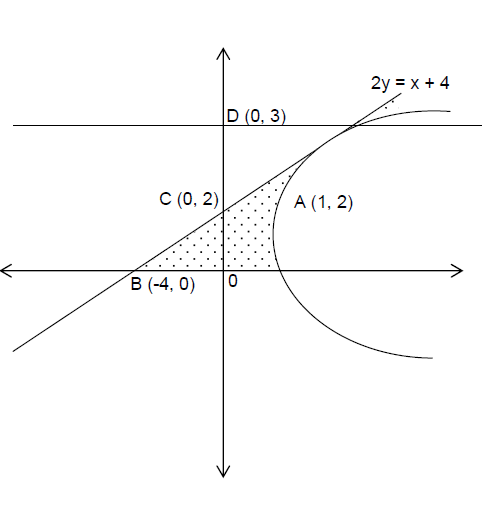
Q. The area of the region bounded by the parabola $(y-2)^2=x-1$ , the tangent to the parabola at the point $(2, 3)$ and the $x$-axis is
AIEEEAIEEE 2009Application of Integrals
Solution:
Equation of tangent at (2, 3) to
$(y-2)^2=x-1$ is $S_1=0$
$⇒ x − 2y + 4 = 0$
Required Area = Area of $ΔOCB +$ Area of $OAPD -$ Area of $ΔPCD$
$=\frac{1}{2}\left(4\times2\right)+$ $\int\limits^{3}_{{0}}(y^2-4y+5)dy-$$\frac{1}{2}\left(1\times2\right)$
$=4+\left[\frac{y^{3}}{3}-2y^{2}+5y\right]^{^{^3}}_{_{_0}}-1=4-9-18+15+-1$
$=28-19=9 $ sq. units
(or)
Area $=\int\limits^{3}_{{0}}(2y-4-y^2+4y-5)dy-\int\limits^{3}_{{0}}(y^2+6y-5)dy=-$$\int\limits^{3}_{{0}}(3-y)^2\,dy$$=\left[\frac{\left(y-3\right)^{3}}{3}\right]^{^{^3}}_{_{_0}}=\frac{27}{3}=9$ sq.units