Q.
Six have to be placed in the square of a given figure such that each row contains at least one . Then, number of ways of doing so are
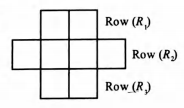
Solution:
As all are identical, In the problem, we need to select squares from , so that no row remains empty.
This can be done as follows :
Number of selections
1
4
1
1
3
2
2
3
1
2
2
2
Hence, total no. of ways
Alternative Solution:
Required number of ways = Coefficient of in the product of the series for above cases = Coefficient of in ((number of ways of filling at least one box out of two for first row (at least one box out of for nd row (at least one out of for third row ))
Coefficient of in
(As and has same ways of filling at least one box)
Coefficient of in
Coefficient of in
Coefficient of in
Short Cut Method :
Total number of squares
Number of places to be filled
Number of ways to do so
These cases also hold those two cases in which either , or may not have any , so exclude these two cases from total ways.
Required number of ways
| Number of selections | |||
|---|---|---|---|
| 1 | 4 | 1 | |
| 1 | 3 | 2 | |
| 2 | 3 | 1 | |
| 2 | 2 | 2 |