Q.
Six $X's$ have to be placed in the square of a given figure such that each row contains at least one $X$. Then, number of ways of doing so are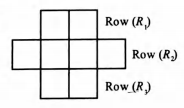
Permutations and Combinations
Solution:
As all $X's$ are identical, In the problem, we need to select $6$ squares from $8$, so that no row remains empty.
This can be done as follows :
$R_1$
$R_2$
$R_3$
Number of selections
1
4
1
$\,{}^{2}C_{1}\cdot\,{}^{4}C_{4}\cdot\,{}^{2}C_{1} = 4$
1
3
2
$\,{}^{2}C_{1}\cdot\,{}^{4}C_{3}\cdot\,{}^{2}C_{2} = 8$
2
3
1
$\,{}^{2}C_{2}\cdot\,{}^{4}C_{3}\cdot\,{}^{2}C_{1} = 8$
2
2
2
$\,{}^{2}C_{2}\cdot\,{}^{4}C_{2}\cdot\,{}^{2}C_{2} = 6$
Hence, total no. of ways $= 4 + 8 + 8 + 6 = 26$
Alternative Solution:
Required number of ways = Coefficient of $x^6$ in the product of the series for above cases = Coefficient of $x^6$ in ((number of ways of filling at least one box out of two for first row $R_1) \times$ (at least one box out of $4$ for $2$nd row $R_2) \times$ (at least one out of $2$ for third row $R_3$))
$=$ Coefficient of $x^6$ in $(\,{}^2C_0x^0 + \,{}^2C_1x^1 + \,{}^2C_2x^2 - 1)^2 \times (\,{}^4C_0 x^0$
$+ \,{}^4C_1x^1 + \,{}^4C_2 x^2 + ... + \,{}^4C_4x^4 - 1)$
(As $R_1$ and $R_3$ has same ways of filling at least one box)
$=$ Coefficient of $x^6$ in $x^3 (2 + x)^2 (4 + 6x + 4x^2 + x^3)$
$=$ Coefficient of $x^{6-3}$ in $(4 + 4x + x^2) (4 + 6x + 4x^2 + x^3)$
$=$ Coefficient of $x^3$ in $(16 + 4x^3 + 16x^3 + 6x^3 + ...)$
$= 4+16 + 6 =26$
Short Cut Method :
Total number of squares $= 8$
Number of places to be filled $= 6$
$\therefore $ Number of ways to do so $= \,{}^8C_6$
$= \,{}^8C_2 = 28$
These $28$ cases also hold those two cases in which either $R_1$, or $R_3$ may not have any $X$, so exclude these two cases from total $28$ ways.
$\therefore $ Required number of ways $= 28 - 2 = 26$
| $R_1$ | $R_2$ | $R_3$ | Number of selections |
|---|---|---|---|
| 1 | 4 | 1 | $\,{}^{2}C_{1}\cdot\,{}^{4}C_{4}\cdot\,{}^{2}C_{1} = 4$ |
| 1 | 3 | 2 | $\,{}^{2}C_{1}\cdot\,{}^{4}C_{3}\cdot\,{}^{2}C_{2} = 8$ |
| 2 | 3 | 1 | $\,{}^{2}C_{2}\cdot\,{}^{4}C_{3}\cdot\,{}^{2}C_{1} = 8$ |
| 2 | 2 | 2 | $\,{}^{2}C_{2}\cdot\,{}^{4}C_{2}\cdot\,{}^{2}C_{2} = 6$ |