Question

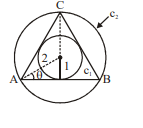
Let $z\in C$ satisfies the equation $\left|\frac{z+\overline{z}}{2\mathrm{Re}(z)}\right|-|z|=\frac{2}{|\overline{z}|}-\left|\frac{z-\overline{z}}{\mathrm{Im}(z)}\right|$.
If locus of $z$ is curve $C_1$ or $C_2(C_1$ lies in $C_2)$ and chord $AB$ of curve $C_2$ touches $C_1$ and from $A$ and $B$ two tangents are drawn to $C_1$ which meet at $C$ lying on $C_2$ and if area of $△ABC=\sqrt{k}$, then find the value of $\left[\frac{k}{4}\right]$.
[Note: $[y]$ denotes greatest integer less than or equal to $y$.

Answer 1

Answer: 6

$\left|\frac{z+\bar{z}}{2R(z)}\right|-|z|=\frac{2}{|\bar{z}|}-\left|\frac{z-\bar{z}}{\mathrm{Im}(z)}\right|$
$1=|z|+\frac{2}{|\bar{z}|}-2$
$|z|+\frac{2}{|\bar{z}|}=3\Rightarrow |z{|}^2-3|z|+2=0\Rightarrow |z|=1\text{ or }|z|=2$
From the figure
$\sin \theta =\frac{1}{2}\Rightarrow \theta =30^{\circ }\Rightarrow △ABC$ is equilateral $AB=2\sqrt{3}$
$\therefore \mathrm{Ar}(△ABC)=\frac{\sqrt{3}}{4}\cdot 4\cdot 3=\sqrt{27}=\sqrt{k}$
$\therefore \left[\frac{k}{4}\right]=\left[\frac{27}{4}\right]=6\text{ Ans. }]$