Question

Let $z \in C$ satisfies the equation $\left|\frac{ z +\overline{ z }}{2 \operatorname{Re}( z )}\right|-| z |=\frac{2}{|\overline{ z }|}-\left|\frac{ z -\overline{ z }}{\operatorname{Im}( z )}\right|$.
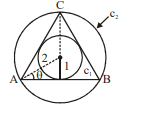
If locus of $z$ is curve $C _1$ or $C _2\left( C _1\right.$ lies in $\left.C _2\right)$ and chord $AB$ of curve $C _2$ touches $C _1$ and from $A$ and $B$ two tangents are drawn to $C_1$ which meet at $C$ lying on $C_2$ and if area of $\triangle A B C=\sqrt{k}$, then find the value of $\left[\frac{k}{4}\right]$.
[Note: $[y]$ denotes greatest integer less than or equal to $y$.

Answer 1

$\left|\frac{z+\bar{z}}{2 R(z)}\right|-|z|=\frac{2}{|\bar{z}|}-\left|\frac{z-\bar{z}}{\operatorname{Im}(z)}\right| $
$1=|z|+\frac{2}{|\bar{z}|}-2$
$|z|+\frac{2}{|\bar{z}|}=3 \Rightarrow|z|^2-3|z|+2=0 \Rightarrow|z|=1 \text { or }|z|=2$
From the figure
$\sin \theta=\frac{1}{2} \Rightarrow \theta=30^{\circ} \Rightarrow \triangle ABC$ is equilateral $AB =2 \sqrt{3}$
$\therefore \operatorname{Ar}(\triangle ABC )=\frac{\sqrt{3}}{4} \cdot 4 \cdot 3=\sqrt{27}=\sqrt{ k } $
$\left.\therefore\left[\frac{ k }{4}\right]=\left[\frac{27}{4}\right]=6 \text { Ans. }\right]$