Question

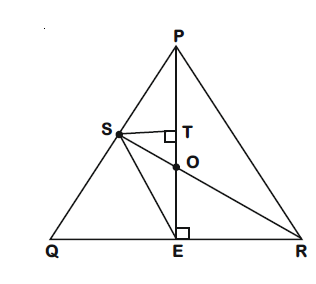
In a non-right-angled triangle $\Delta PQR,$ let $p,q,r$ denote the lengths of the sides opposite to the angles at P, Q, R respectively. The median from $R$ meets the side $PQ$ at $S$, the perpendicular from $P$ meets the side $QR$ at $E$, and RS and $PE$ intersect at $O$. If $p=\sqrt{3},q=1,$ and the radius of the circumcircle of the $\Delta PQR$ equals 1, then which of the following options is/are correct?

• A. Length of $RS=\frac{\sqrt{7}}{2}$
• B. Area of $\Delta SOE=\frac{\sqrt{3}}{12}$
• C. Length of $OE\frac{1}{6}$
• D. Radius of incircle of $\Delta PQR=\frac{\sqrt{3}}{2}\left(2-\sqrt{3}\right)$

Answer 1

Answer: (A), (C), (D)

$\because \frac{p}{sinP}=\frac{q}{sinQ}=\frac{r}{sinR}=2\times$ circumradius (sine rule)
$\Rightarrow \frac{\sqrt{3}}{sinP}=\frac{1}{sinQ}=\frac{r}{sinR}=2$
Clearly, $P=120^{\circ },Q=30^{\circ }$ and $R=30^{\circ }$
So $PQR$ is an isosceles triangle.
$r=1$ and $PE$ is also a median, so point $‘O’$ is centroid.
(A) Area of $\Delta SOE=\frac{1}{2}OE\times ST$
$=\frac{1}{2}\times \frac{1}{6}\times PSsin60^{\circ }$
$=\frac{1}{12}\times \frac{1}{2}\times \frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}}{48}$
(B) From Apollonius theorem
$2\left(P{S}^2+R{S}^2\right)=P{R}^2+Q{R}^2\Rightarrow 2\left(\frac{1}{4}+R{S}^2\right)=1+3\Rightarrow RS=\frac{\sqrt{7}}{2}$
(C) Again from Apollonius theorem
$2\left(P{E}^2+Q{E}^2\right)=P{Q}^2+P{R}^2\Rightarrow 2\left(P{E}^2+\frac{3}{4}\right)=1+1\Rightarrow PE=\frac{1}{2}$
Also $OE=\frac{1}{3}PE=\frac{1}{6}$
(D) Inradius $=\frac{\Delta }{S}=\frac{\frac{1}{2}pqsinR}{\frac{1}{2}\left(p+q+r\right)}=\frac{\sqrt{3}\times 1\times \frac{1}{2}}{1+1+\sqrt{3}}=\frac{\sqrt{3}}{2}\left(2-\sqrt{3}\right)$