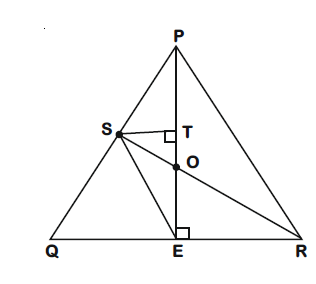
Q. In a non-right-angled triangle $\Delta PQR,$ let $p, q, r$ denote the lengths of the sides opposite to the angles at P, Q, R respectively. The median from $R$ meets the side $PQ$ at $S$, the perpendicular from $P$ meets the side $QR$ at $E$, and RS and $PE$ intersect at $O$. If $p=\sqrt{3}, q=1,$ and the radius of the circumcircle of the $\Delta PQR$ equals 1, then which of the following options is/are correct?
JEE AdvancedJEE Advanced 2019
Solution:
$\because \frac{p}{sin\,P}=\frac{q}{sin\,Q}=\frac{r}{sin\,R}=2\, \times$ circumradius (sine rule)
$\Rightarrow \frac{\sqrt{3}}{sin\,P} =\frac{1}{sin\,Q}=\frac{r}{sinR}=2$
Clearly, $P =120^{\circ}, Q=30^{\circ}$ and $R=30^{\circ}$
So $PQR$ is an isosceles triangle.
$r = 1$ and $PE$ is also a median, so point $‘O’$ is centroid.
(A) Area of $\Delta SOE=\frac{1}{2}OE\times ST$
$=\frac{1}{2}\times\frac{1}{6}\times PS\,sin\,60^{\circ}$
$=\frac{1}{12}\times\frac{1}{2}\times\frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}}{48}$
(B) From Apollonius theorem
$2\left(PS^{2}+RS^{2}\right)=PR^{2}+QR^{2} \Rightarrow 2\left(\frac{1}{4}+RS^{2}\right)=1+3 \Rightarrow RS=\frac{\sqrt{7}}{2}$
(C) Again from Apollonius theorem
$2\left(PE^{2}+QE^{2}\right)=PQ^{2}+PR^{2} \Rightarrow 2\left(PE^{2}+\frac{3}{4}\right)=1+1 \Rightarrow PE=\frac{1}{2}$
Also $OE=\frac{1}{3}PE=\frac{1}{6}$
(D) Inradius $=\frac{\Delta}{S}=\frac{\frac{1}{2}pqsinR}{\frac{1}{2}\left(p+q+r\right)}=\frac{\sqrt{3}\times1\times\frac{1}{2}}{1+1+\sqrt{3}}=\frac{\sqrt{3}}{2}\left(2-\sqrt{3}\right)$