Question

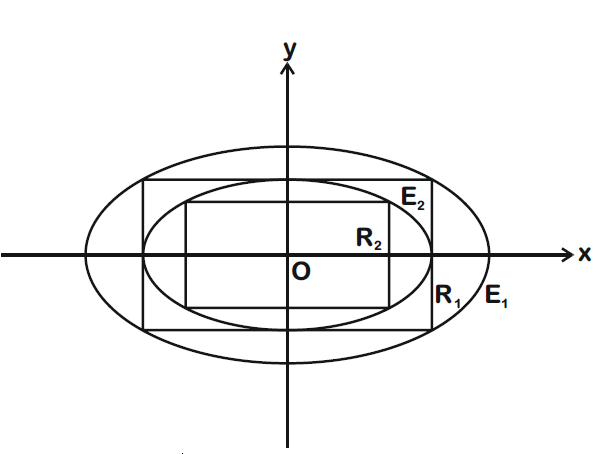
Define the collections {$E_1,E_2,E_3$,... } of ellipses and {$R_1,R_2,R_3$,...} of rectangles as follows: $E_1:\frac{x^2}{9}+\frac{y^2}{4}=1;$
i?$R_1$: rectangle of largest area, with sides parallel to the axes, inscribed in $E_1$;
$E_n$: ellipse $\frac{x^2}{a_n^2}+\frac{y^2}{b_n^2}=1$ of largest area inscribed in $R_{n-1},n>1;$
$R_n$: rectangle of largest area, with sides parallel to the axes, inscribed in $E_n,n>1$.
Then which of the following options is/are correct?

• A. The eccentricities of $E_{18}and{E}_{19}$ are NOT equal
• B. $\sum _{n=1}^N$(area of $R_n$) $<24$, for each positive integer $N$
• C. The length of latus rectum of $E_9$ is $\frac{1}{6}$
• D. The distance of a focus from the centre in $E_9$ is $\frac{\sqrt{5}}{32}$

Answer 1

Answer: (B), (C)

$E_1=\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$\left(Herea=3andb=2\right)$
Let a vertex of $R_1$ be (acos$\theta$, bsin$\theta$)
Area of $R_1$ = 2acos$\theta$ × 2bsin$\theta$
$=2absin2\theta$
Area of $R_1$ will be maximum if
$\theta =\frac{\pi }{4}$
So, maximum area of $R_1=2ab$
Now, ellipse $E_2$ will have semi-major axis $\frac{a}{\sqrt{2}}$ and semi-minor axis $\frac{b}{\sqrt{2}}$
$E_2:\frac{x^2}{{\left(\frac{a}{\sqrt{2}}\right)}^2}+\frac{y^2}{{\left(\frac{b}{\sqrt{2}}\right)}^2}=1;$ maximum area of $R_2=2\left(\frac{a}{\sqrt{2}}\right)\left(\frac{b}{\sqrt{2}}\right)$
Similarly $E_3:\frac{x^2}{\left(\frac{a}{{\left(\sqrt{2}\right)}^2}\right)}+\frac{y^2}{\left(\frac{b}{{\left(\sqrt{2}\right)}^2}\right)}=1$ and so on.
So, $E_n:\frac{x^2}{{\left(\frac{a}{{\left(\sqrt{2}\right)}^{n-1}}\right)}^2}+\frac{y^2}{{\left(\frac{b}{{\left(\sqrt{2}\right)}^{n-1}}\right)}^2}=1$
and maximum area of $R_n=2\left(\frac{a}{{\left(\sqrt{2}\right)}^{n-1}}\right)\left(\frac{b}{{\left(\sqrt{2}\right)}^{n-1}}\right)$
(A) All ellipse have same eccentricity because the ratio of semi-major axis and semi-minor axis is same for all ellipses.
$e=\sqrt{1-\frac{b_n^2}{a_n^2}}=\sqrt{1-\frac{b^2}{a^2}}=\frac{\sqrt{5}}{3}$
(B) Length of latus rectum of $E_n=\frac{2b_n^2}{a_n^2}=\frac{2b^2}{a{\left(\sqrt{2}\right)}^{n-1}}$
Length of latus rectum of $E_9=\frac{2\times 4}{3\times {\left(\sqrt{2}\right)}^{9-1}}=\frac{1}{6}$
(C) $\sum _{n=1}^m$ area of rectangle $R_n<$ area of $R_1+$ area of $R_2+\dots \dots \infty$
$\sum _{n=1}^m$ area of rectangle $R_n<2ab+2\left(\frac{a}{\sqrt{2}}\right)\left(\frac{b}{\sqrt{2}}\right)+2\left(\frac{a}{{\left(\sqrt{2}\right)}^2}\right)\left(\frac{b}{{\left(\sqrt{2}\right)}^2}\right)+.......\infty$
$\sum _{n=1}^m$ area of rectangle $R_n<2ab\left[1+\frac{1}{2}+\frac{1}{2^2}+.......\infty \right]$
$\sum _{n=1}^m$ area of rectangle $R_n<12\left[\frac{1}{1-\frac{1}{2}}\right]$
$\sum _{n=1}^m$ area of rectangle $R_n<24$
(D) Distance between focus and centre of $E_9=a_9.e$
$=\frac{a}{{\left(\sqrt{2}\right)}^8}\cdot e=\frac{3}{2^4}\cdot \frac{\sqrt{5}}{3}=\frac{\sqrt{5}}{16}$