Question

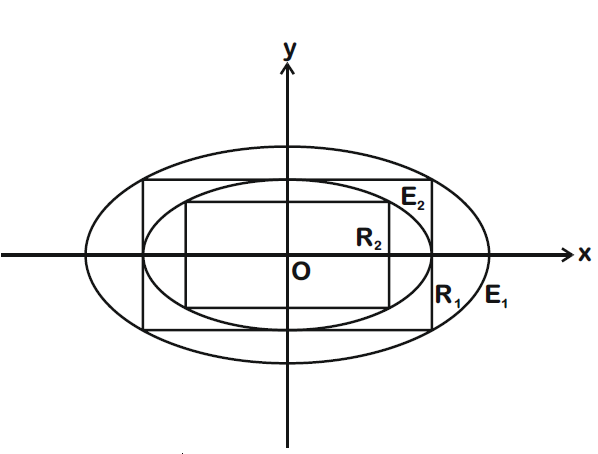
Define the collections {$E_1, E_2, E_3$,... } of ellipses and {$R_1,R_2, R_3$,...} of rectangles as follows: $E_{1}: \frac{x^{2}}{9}+\frac{y^{2}}{4}=1;$
i?$R_1$: rectangle of largest area, with sides parallel to the axes, inscribed in $E_1$;
$E_n$: ellipse $\frac{x^{2}}{a^{2}_{n}}+\frac{y^{2}}{b^{2}_{n}}=1$ of largest area inscribed in $R_{n-1}, n > 1;$
$R_n$: rectangle of largest area, with sides parallel to the axes, inscribed in $E_n, n > 1$.
Then which of the following options is/are correct?

• A. The eccentricities of $E_{18} and E_{19}$ are NOT equal
• B. $ \displaystyle \sum_{n=1}^N$(area of $R_n$) $< 24$, for each positive integer $N$
• C. The length of latus rectum of $E_9$ is $\frac{1}{6}$
• D. The distance of a focus from the centre in $E_9$ is $\frac{\sqrt{5}}{32}$

Answer 1

Answer: (B), (C)

$E_{1}=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\,\,$$\left(Here\, a = 3\, and \,b = 2\right)$
Let a vertex of $R_1$ be (acos$\theta$, bsin$\theta$)
Area of $R_1$ = 2acos$\theta$ × 2bsin$\theta$
$= 2absin2\theta$
Area of $R_1$ will be maximum if
$\theta=\frac{\pi}{4}$
So, maximum area of $R_1 = 2ab$
Now, ellipse $E_2$ will have semi-major axis $\frac{a}{\sqrt{2}}$ and semi-minor axis $\frac{b}{\sqrt{2}}$
$E_{2}: \frac{x^{2}}{\left(\frac{a}{\sqrt{2}}\right)^{2}}+\frac{y^{2}}{\left(\frac{b}{\sqrt{2}}\right)^{2}}=1;$ maximum area of $R_{2}=2\left(\frac{a}{\sqrt{2}}\right)\left(\frac{b}{\sqrt{2}}\right)$
Similarly $E_{3}: \frac{x^{2}}{\left(\frac{a}{\left(\sqrt{2}\right)^{2}}\right)}+\frac{y^{2}}{\left(\frac{b}{\left(\sqrt{2}\right)^{2}}\right)}=1$ and so on.
So, $E_{n}: \frac{x^{2}}{\left(\frac{a}{\left(\sqrt{2}\right)^{n-1}}\right)^{2}}+\frac{y^{2}}{\left(\frac{b}{\left(\sqrt{2}\right)^{n-1}}\right)^{2}}=1$
and maximum area of $R_{n}=2\left(\frac{a}{\left(\sqrt{2}\right)^{n-1}}\right)\left(\frac{b}{\left(\sqrt{2}\right)^{n-1}}\right)$
(A) All ellipse have same eccentricity because the ratio of semi-major axis and semi-minor axis is same for all ellipses.
$e=\sqrt{1-\frac{b^{2}_{n}}{a^{2}_{n}}}=\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{\sqrt{5}}{3}$
(B) Length of latus rectum of $E_{n}=\frac{2b^{2}_{n}}{a^{2}_{n}}=\frac{2b^{2}}{a\left(\sqrt{2}\right)^{n-1}}$
Length of latus rectum of $E_{9}=\frac{2\times4}{3\times\left(\sqrt{2}\right)^{9-1}}=\frac{1}{6}$
(C) $\displaystyle \sum_{n=1}^m $ area of rectangle $R_n <$ area of $R_1 +$ area of $R_2 + …… \infty$
$\displaystyle \sum_{n=1}^m $ area of rectangle $R_{n}< 2ab+2\left(\frac{a}{\sqrt{2}}\right)\left(\frac{b}{\sqrt{2}}\right)+2\left(\frac{a}{\left(\sqrt{2}\right)^{2}}\right)\left(\frac{b}{\left(\sqrt{2}\right)^{2}}\right)+....... \infty$
$\displaystyle \sum_{n=1}^m $ area of rectangle $R_{n}< 2ab\left[1+\frac{1}{2}+\frac{1}{2^{2}}+....... \infty\right]$
$\displaystyle \sum_{n=1}^m $ area of rectangle $R_{n}< 12\left[\frac{1}{1-\frac{1}{2}}\right]$
$\displaystyle \sum_{n=1}^m $ area of rectangle $R_{n}<24$
(D) Distance between focus and centre of $E_9 = a_9.e$
$=\frac{a}{\left(\sqrt{2}\right)^{8}}\cdot e=\frac{3}{2^{4}}\cdot\frac{\sqrt{5}}{3}=\frac{\sqrt{5}}{16}$