Question

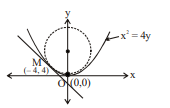
Consider the parabola $x^2=4y$ and circle $x^2+(y-5{)}^2=r^2(r>0)$. Given that the circle touches the parabola at the points $P$ and $Q$. Let $R$ be the point of intersection of tangents to parabola at $P$ and $Q$ and $S$ be the centre of circle.
The equation of the circle which passes through the vertex of the parabola $x^2=4y$ and touches it at the point $M(-4,4)$, is

• A. $x^2+y^2-10x-18y=0$
• B. $x^2+y^2-8x-16y=0$
• C. $x^2+y^2+8x=0$
• D. $x^2+y^2-8y=0$

Answer 1

Answer: (B)

The equation of tangent at $M(-4,4)$ to the parabola $x^2=4y$, is
$x(-4)=2(y+4)\Rightarrow 2x+y+4=0$
Let the required circle be $(x+4{)}^2+(y-4{)}^2+\lambda (2x+y+4)=0$
As above circle passes through $(0,0)$, so $16+16+\lambda (4)=0$
$\Rightarrow 4\lambda =-32\Rightarrow \lambda =-8$
Hence required equation of circle is $x^2+y^2-8x-16y=0$