Q.
Consider the parabola $x^2=4 y$ and circle $x^2+(y-5)^2=r^2(r>0)$. Given that the circle touches the parabola at the points $P$ and $Q$. Let $R$ be the point of intersection of tangents to parabola at $P$ and $Q$ and $S$ be the centre of circle.
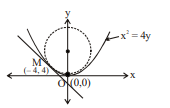
The equation of the circle which passes through the vertex of the parabola $x^2=4 y$ and touches it at the point $M(-4,4)$, is
Conic Sections
Solution: