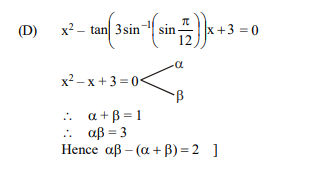- Tardigrade
- Question
- Mathematics
- Consider f(x)= tan -1(((√12-2) x2/x4+2 x2+3)) and m and M are respectively minimum and maximum values of f(x) and x=a(a>0) is the point in the domain of f(x) where f(x) attains its maximum value. Column I Column II A If sin -1 2 √x=3 tan -1( tan (m+M)) then 8 x equals P 0 B If cos -1 x+ cos -1 y=3 tan -1( tan (7 M /2))+ tan -1( m + tan (3 π/8)) then (x+y) equals Q 2 C The value of tan ( sec -1((2/ a 2))+ M ) equals( R - 2 D If α and β are roots of the equation x2-( tan (3 sin -1( sin M ))) x+ a 4=0, then α β-(α+β) equals S 1 T -1
Q.
Consider and and are respectively minimum and maximum values of and is the point in the domain of where attains its maximum value.
Column I
Column II
A
If then equals
P
0
B
If then equals
Q
2
C
The value of equals(
R
- 2
D
If and are roots of the equation , then equals
S
1
T
-1
| Column I | Column II | ||
|---|---|---|---|
| A | If then equals | P | 0 |
| B | If then equals | Q | 2 |
| C | The value of equals( | R | - 2 |
| D | If and are roots of the equation , then equals | S | 1 |
| T | -1 | ||
Solution:
We have
As (UsingA.M.-GM. inequality)
,
which occurs at , which occurs at
(A)
(B)
(C)
(D)