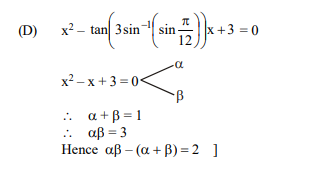Q.
Consider $f(x)=\tan ^{-1}\left(\frac{(\sqrt{12}-2) x^2}{x^4+2 x^2+3}\right)$ and $m$ and $M$ are respectively minimum and maximum values of $f(x)$ and $x=a(a>0)$ is the point in the domain of $f(x)$ where $f(x)$ attains its maximum value.
Column I
Column II
A
If $\sin ^{-1} 2 \sqrt{x}=3 \tan ^{-1}(\tan (m+M))$ then $8 x$ equals
P
0
B
If $\cos ^{-1} x+\cos ^{-1} y=3\left\{\tan ^{-1}\left(\tan \frac{7 M }{2}\right)+\tan ^{-1}\left( m +\tan \frac{3 \pi}{8}\right)\right\}$ then $(x+y)$ equals
Q
2
C
The value of $\tan \left(\sec ^{-1}\left(\frac{2}{ a ^2}\right)+ M \right)$ equals(
R
- 2
D
If $\alpha$ and $\beta$ are roots of the equation $x^2-\left(\tan \left(3 \sin ^{-1}(\sin M )\right)\right) x+ a ^4=0$, then $\alpha \beta-(\alpha+\beta)$ equals
S
1
T
-1
| Column I | Column II | ||
|---|---|---|---|
| A | If $\sin ^{-1} 2 \sqrt{x}=3 \tan ^{-1}(\tan (m+M))$ then $8 x$ equals | P | 0 |
| B | If $\cos ^{-1} x+\cos ^{-1} y=3\left\{\tan ^{-1}\left(\tan \frac{7 M }{2}\right)+\tan ^{-1}\left( m +\tan \frac{3 \pi}{8}\right)\right\}$ then $(x+y)$ equals | Q | 2 |
| C | The value of $\tan \left(\sec ^{-1}\left(\frac{2}{ a ^2}\right)+ M \right)$ equals( | R | - 2 |
| D | If $\alpha$ and $\beta$ are roots of the equation $x^2-\left(\tan \left(3 \sin ^{-1}(\sin M )\right)\right) x+ a ^4=0$, then $\alpha \beta-(\alpha+\beta)$ equals | S | 1 |
| T | -1 | ||
Inverse Trigonometric Functions
Solution:
We have $f(x)=\tan ^{-1}\left(\frac{2(\sqrt{3}-1)}{x^2+\frac{3}{x^2}+2}\right)$
As $x^2+\frac{3}{x^2} \geq 2 \sqrt{3} $ (UsingA.M.-GM. inequality)
$\Rightarrow x^2+\frac{3}{x^2}+2 \geq 2+2 \sqrt{3}$
$\left.\therefore f ( x )\right|_{\max }=\tan ^{-1}\left(\frac{2(\sqrt{3}-1)}{2(\sqrt{3}+1)}\right)=\frac{\pi}{12}= M$,
which occurs at $x ^2=\frac{3}{ x ^2} \Rightarrow x =3^{\frac{1}{4}}= a$ $\left. f ( x )\right|_{\text {min }}=0= m$, which occurs at $x =0$
(A)$\sin ^{-1}(2 \sqrt{x})=3 \tan ^{-1}\left(\tan \frac{\pi}{12}\right)=\frac{\pi}{4} $
$2 \sqrt{x}=\frac{1}{\sqrt{2}} \Rightarrow 8 x=1$
(B) $\cos ^{-1} x +\cos ^{-1} y =3\left[\tan ^{-1}\left(\tan \frac{7 \pi}{24}\right)+\tan ^{-1}\left(0+\tan \frac{3 \pi}{8}\right)\right]=3\left[\frac{7 \pi}{24}+\frac{3 \pi}{8}\right]=3\left(\frac{16 \pi}{24}\right)=2 \pi $
$\therefore x = y =-1 \Rightarrow x + y =-2$
(C) $ \tan \left(\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)+\frac{\pi}{12}\right)=\tan \left(\frac{\pi}{6}+\frac{\pi}{12}\right)=1$
(D) $x ^2-\tan \left(3 \sin ^{-1}\left(\sin \frac{\pi}{12}\right)\right) x +3=0$