Question

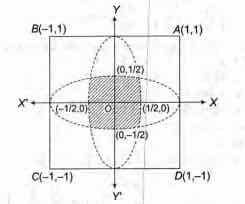
Consider a square with vertices at (1,1), (-1, 1), (-1, -1)
and (1, -1). If S is the region consisting of all points
inside the square which are nearer to the origin than to
any edge. Then, sketch the region S and find its area.

Answer 1

The equations of the sides of the square are as follow :
AB:y = 1, BC : x = - l , CD :y = - 1, DA : x= 1
Let the region be S and (x, y) is any point inside it.
Then, according to given conditions,
$\sqrt{x^2+y^2}<|1-x|,|1+x|,|1-y|,|1+y|,$
$\Rightarrow$ $x^2+y^2<(1-x{)}^2,(1+x{)}^2,(1-y{)}^2,(1+y{)}^2$
$\Rightarrow$ $x^2+y^2<x^2-2x+1,x^2+2x+1,$ $y^2-2y+1,Y^2+2y+1$
$\Rightarrow$ $y^2<1-2x,y^2<1+2x,x^2<1-2yand{x}^2<2y+1$
Now, in $y^2=1-2x$ and $y^2=1+2x$, the first equation
represents a parabola with vertex at ($\frac{1}{2}$, 0) and second
equation represents a parabola with vertex ($-\frac{1}{2}$, 0)
and in $x^2=1-2y$ and $x^2=1+2y$, the first equation
represents a parabola with vertex at (0, $\frac{1}{2}$) and second
equation represents a parabola with vertex at (0, - $\frac{1}{2}$).
Therefore, the region S is lying inside the four parabolas
$y^2=1-2x$, $y^2=1+2x$, $x^2=1+2y$, $x^2=1-2y$
where, S is the shaded region.
Now, S is symmetrical in all four quadrants, therefore
S = 4 x Area lying in the first quadrant.
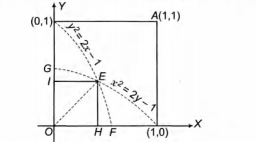
Now, $y^2=1-2x$ and $x^2=1-2y$ intersect on the line
y = x The point of intersection is E($\sqrt{2}$-1, $\sqrt{2}$-1).
Area of the region OEFO
= Area of $△$ OEH + Area of HEFH
= $\frac{1}{2}(\sqrt{2}-1{)}^2$ + ${\int }_{\sqrt{2}-1}^{\frac{1}{2}}\sqrt{1-2x}dx$
= $\frac{1}{2}(\sqrt{2}-1{)}^2$ + $[(1-2x{)}^{\frac{3}{2}}\frac{2}{3}.\frac{1}{2}\frac{1}{2}(-1){]}_{\sqrt{2}-1}^{\frac{1}{2}}$
=$\frac{1}{2}(2+1-2\sqrt{2})+\frac{1}{3}(1+2-2\sqrt{2})\frac{3}{2}$
=$\frac{1}{2}(3-2\sqrt{2})$ +$\frac{1}{3}(3-2\sqrt{2}{)}^{\frac{3}{2}}$
=$\frac{1}{2}(3-2\sqrt{2})$ +$\frac{1}{3}(\sqrt{2}-1{)}^3$
=$\frac{1}{2}(3-\sqrt{2})$ + $\frac{1}{3}[2\sqrt{2}-1-3\sqrt{2}(\sqrt{2}-1)]$
=$\frac{1}{2}(3-2\sqrt{2})$ + $\frac{1}{3}[5\sqrt{2}-7]$
=$\frac{1}{6}[9-6\sqrt{2}+10\sqrt{2}-14]$= $\frac{1}{6}[4\sqrt{2}-5]$ sq units
Similarly, area OEGO = $\frac{1}{6}[4\sqrt{2}-5]$ sq units
Therefore, area of S lying in first quadrant
$=\frac{2}{6}(4\sqrt{2}-5)$=$=\frac{1}{3}(4\sqrt{2}-5)$ sq units
Hence, S$=\frac{4}{3}(4\sqrt{2}-5)$=$=\frac{1}{3}(16\sqrt{2}-20)$ sq units