Q.
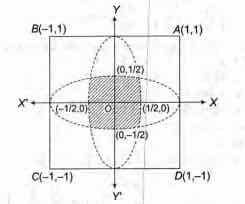
Consider a square with vertices at (1,1), (-1, 1), (-1, -1)
and (1, -1). If S is the region consisting of all points
inside the square which are nearer to the origin than to
any edge. Then, sketch the region S and find its area.
IIT JEEIIT JEE 1995
Solution:
The equations of the sides of the square are as follow :
AB:y = 1, BC : x = - l , CD :y = - 1, DA : x= 1
Let the region be S and (x, y) is any point inside it.
Then, according to given conditions,
$\sqrt{x^2+y^2} < |1-x|, |1+x|, |1-y|, |1+y|,$
$\Rightarrow $ $x^2+y^2 <(1-x)^2, (1+x)^2, (1-y)^2, (1+y)^2$
$\Rightarrow $ $x^2+y^2 < x^2-2x+1, x^2+2x+1,$ $y^2-2y+1, Y^2+2y+1$
$\Rightarrow $ $y^2<1-2x, y^2<1+2x, x^2<1-2y and x^2<2y+1$
Now, in $y^2=1-2x$ and $y^2=1+2x$, the first equation
represents a parabola with vertex at ($\frac {1}{2}$, 0) and second
equation represents a parabola with vertex ($-\frac {1}{2}$, 0)
and in $x^2=1-2y$ and $x^2=1+2y$, the first equation
represents a parabola with vertex at (0, $\frac {1}{2}$) and second
equation represents a parabola with vertex at (0, - $\frac {1}{2}$).
Therefore, the region S is lying inside the four parabolas
$y^2=1-2x$, $y^2=1+2x$, $x^2=1+2y$, $x^2=1-2y$
where, S is the shaded region.
Now, S is symmetrical in all four quadrants, therefore
S = 4 x Area lying in the first quadrant.
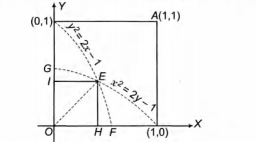
Now, $y^2=1-2x$ and $x^2=1-2y$ intersect on the line
y = x The point of intersection is E($\sqrt2$-1, $\sqrt2$-1).
Area of the region OEFO
= Area of $\triangle$ OEH + Area of HEFH
= $\frac {1}{2}(\sqrt2-1)^2$ + $\int_{\sqrt2-1}^{\frac {1}{2}}{\sqrt{1-2x}} dx$
= $\frac {1}{2}(\sqrt2-1)^2$ + $\bigg [ (1 - 2x)^{\frac {3}{2}} \frac {2}{3} . {\frac {1}{2}}\frac {1}{2}(-1) \bigg]_{\sqrt2-1}^\frac {1}{2}$
=$\frac {1}{2}(2+1-2\sqrt2) + \frac {1}{3}(1+2-2\sqrt2)\frac {3}{2}$
=$\frac {1}{2}(3-2\sqrt2)$ +$\frac {1}{3}(3-2\sqrt2)^\frac {3}{2}$
=$\frac {1}{2}(3-2\sqrt2)$ +$\frac {1}{3}(\sqrt2-1)^{3}$
=$\frac {1}{2}(3-\sqrt2)$ + $\frac {1}{3}[2\sqrt{2}-1-3\sqrt2(\sqrt2-1)]$
=$\frac {1}{2}(3-2\sqrt2)$ + $\frac {1}{3}[ 5\sqrt2-7]$
=$\frac {1}{6}[9-6\sqrt2+10\sqrt2-14]$= $\frac {1}{6}[4\sqrt2-5]$ sq units
Similarly, area OEGO = $\frac {1}{6}[4\sqrt2-5]$ sq units
Therefore, area of S lying in first quadrant
$=\frac {2}{6}(4\sqrt2-5)$=$=\frac {1}{3}(4\sqrt2-5)$ sq units
Hence, S$=\frac {4}{3}(4\sqrt2-5)$=$=\frac {1}{3}(16\sqrt2-20)$ sq units