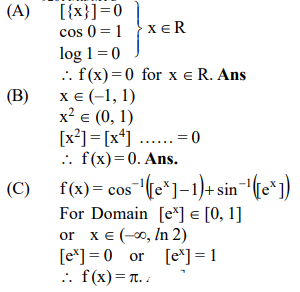- Tardigrade
- Question
- Mathematics
- Column I Column II A Let f(x)=√ log ( cos [ x ]), then f(x) is P Even and Periodic function B Let f :(-1,1) arrow R be defined as f ( x )= displaystyle∑ r =1100[ x 2 r ], then f(x) is Q Bounded C Let f(x)= cos -1([ e x ]-1)+ sin -1([ e x ]), then f(x) is R Domain contains at least one integer and at most 3 integers S Both many one and odd function [Note: [y] and y denote greatest integer and fractional part function of y respectively.]
Q.
Column I
Column II
A
Let , then is
P
Even and Periodic function
B
Let be defined as , then is
Q
Bounded
C
Let , then is
R
Domain contains at least one
integer and at most 3 integers
S
Both many one and odd function
[Note : [y] and denote greatest integer and fractional part function of y respectively.]
| Column I | Column II | ||
|---|---|---|---|
| A | Let , then is | P | Even and Periodic function |
| B | Let be defined as , then is | Q | Bounded |
| C | Let , then is | R | Domain contains at least one integer and at most 3 integers |
| S | Both many one and odd function | ||
Solution:
Correct answer is (d) (A) P, Q, S; (B) P, Q, R, S; (C) Q