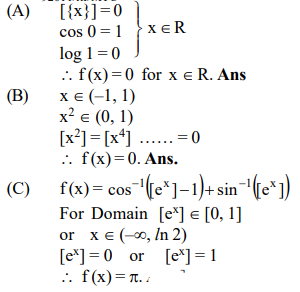Q.
Column I
Column II
A
Let $f(x)=\sqrt{\log (\cos [\{x\}])}$, then $f(x)$ is
P
Even and Periodic function
B
Let $f :(-1,1) \rightarrow R$ be defined as $f ( x )=\displaystyle\sum_{ r =1}^{100}\left[ x ^{2 r }\right]$, then $f(x)$ is
Q
Bounded
C
Let $f(x)=\cos ^{-1}\left(\left[ e ^{ x }\right]-1\right)+\sin ^{-1}\left(\left[ e ^{ x }\right]\right)$, then $f(x)$ is
R
Domain contains at least one
integer and at most 3 integers
S
Both many one and odd function
[Note : [y] and $\{y\}$ denote greatest integer and fractional part function of y respectively.]
| Column I | Column II | ||
|---|---|---|---|
| A | Let $f(x)=\sqrt{\log (\cos [\{x\}])}$, then $f(x)$ is | P | Even and Periodic function |
| B | Let $f :(-1,1) \rightarrow R$ be defined as $f ( x )=\displaystyle\sum_{ r =1}^{100}\left[ x ^{2 r }\right]$, then $f(x)$ is | Q | Bounded |
| C | Let $f(x)=\cos ^{-1}\left(\left[ e ^{ x }\right]-1\right)+\sin ^{-1}\left(\left[ e ^{ x }\right]\right)$, then $f(x)$ is | R | Domain contains at least one integer and at most 3 integers |
| S | Both many one and odd function | ||
Inverse Trigonometric Functions
Solution:
Correct answer is (d) (A) P, Q, S; (B) P, Q, R, S; (C) Q