Question

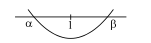
Column I		Column II
A	If ${\log }_{\frac{1}{x}}\left(\frac{2(x-2)}{(x+1)(x-5)}\right)\ge 1$, then $x$ can belongs to	P	$(0,1/3]$
B	If ${\log }_{1/2}(4-x)\ge {\log }_{1/2}2-{\log }_{1/2}(x-1)$, then $x$ can belongs to	Q	$(1,2]$
C	If ${\log }_{3}x-{\log }_3^{2}x\le \frac{3}{2}{\log }_{(1/2\sqrt{2})}4$, then $x$ can belongs to	R	$(3,4)$
D	Let $\alpha$ and $\beta$ are the roots of the quadratic equation$\left(p^2-3p+4\right)x^2-4(2p-1)x+16=0$If $\alpha$ and $\beta$ satisfy the condition $\beta >1>\alpha$, then $p$ can lie in	S	$(3,8)$

• A. (A) Q; (B) Q, R; (C) P; (D) R, P
• B. (A) Q; (B) Q, R; (C) P; (D) R, Q
• C. (A) Q; (B) Q, R; (C) P; (D) R, S
• D. (A) Q; (B) Q, R; (C) P; (D) R, R

Answer 1

Answer: (C)

(A) Let $1/x>1$ i.e. $0<x<1$
${\log }_{\frac{1}{x}}\left(\frac{2(x-2)}{(x+1)(x-5)}\right)\ge 1\Rightarrow \frac{2(x-2)}{(x+1)(x-5)}\ge \frac{1}{x}\Rightarrow \frac{2(x-2)}{(x+1)(x-5)}-\frac{1}{x}\ge 0$
$\frac{2x(x-2)-(x+1)(x-5)}{x(x+1)(x-5)}\ge 0\Rightarrow \frac{x^2+5}{x(x+1)(x-5)}\ge 0$

Hence no solution in this case
now let $0<\frac{1}{x}<1;x>1$
in this case $0<x<5$
its intersection with $x>1$ and the domain of the equation gives $x\in (1,2)\Rightarrow$ (Q)
(B)
${\log }_{1/2}(4-x)\ge {\log }_{1/2}2-{\log }_{1/2}(x-1)$
$(4-x)(x-1)\le 2$
$5x-x^2-4\le 2\Rightarrow x^2-5x+6\ge 0$
$(x-3)(x-2)\ge 0\Rightarrow x\ge 3\text{ or }x\le 2$
${\log }_{1/2}(4-x)(x-1)\ge {\log }_{1/2}2$
but $x\in (1,4)$
Hence final answer is $(1,2]\cup [3,4)\Rightarrow (Q)\&$ (R)
(C) Given: ${\log }_{3}x-{\log }_3^{2}x\le \frac{3}{2}{\log }_{(1/2\sqrt{2})}4$
${\log }_{3}x-{\log }_3^{2}x\le -\frac{3}{2}\frac{{\log }_{2}4}{{\log }_{2}2\sqrt{2}}$
${\log }_{3}x-{\log }_3^{2}x\le -2$
$\text{ put }{\log }_{3}x=y$
$y-y^2\le -2$
$y^2-y-2\ge 0$
$(y-2)(y+1)\ge 0$

$x\le \frac{1}{3}\Rightarrow (0,1/3]\cup [9,\infty )\Rightarrow (P)$
(D) $f(x)=\left(p^2-3p+4\right)x^2-4(2p-1)x+16=0$
1 lies between the roots hence $f(1)<0$

$p^2-3p+4-8p+4+16<0$
$p^2-11p+24<0$
$(p-8)(p-3)<0$
$\Rightarrow p\in (3,8)\Rightarrow (R)\&(S)$