Q.
Column I
Column II
A
If $\log _{\frac{1}{x}}\left(\frac{2(x-2)}{(x+1)(x-5)}\right) \geq 1$, then $x$ can belongs to
P
$(0,1 / 3]$
B
If $\log _{1 / 2}(4-x) \geq \log _{1 / 2} 2-\log _{1 / 2}(x-1)$, then $x$ can belongs to
Q
$(1,2]$
C
If $\log _3 x-\log _3^2 x \leq \frac{3}{2} \log _{(1 / 2 \sqrt{2})} 4$, then $x$ can belongs to
R
$(3,4)$
D
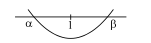
Let $\alpha$ and $\beta$ are the roots of the quadratic equation$\left(p^2-3 p+4\right) x^2-4(2 p-1) x+16=0$If $\alpha$ and $\beta$ satisfy the condition $\beta>1>\alpha$, then $p$ can lie in
S
$(3,8)$
| Column I | Column II | ||
|---|---|---|---|
| A | If $\log _{\frac{1}{x}}\left(\frac{2(x-2)}{(x+1)(x-5)}\right) \geq 1$, then $x$ can belongs to | P | $(0,1 / 3]$ |
| B | If $\log _{1 / 2}(4-x) \geq \log _{1 / 2} 2-\log _{1 / 2}(x-1)$, then $x$ can belongs to | Q | $(1,2]$ |
| C | If $\log _3 x-\log _3^2 x \leq \frac{3}{2} \log _{(1 / 2 \sqrt{2})} 4$, then $x$ can belongs to | R | $(3,4)$ |
| D | Let $\alpha$ and $\beta$ are the roots of the quadratic equation$\left(p^2-3 p+4\right) x^2-4(2 p-1) x+16=0$If $\alpha$ and $\beta$ satisfy the condition $\beta>1>\alpha$, then $p$ can lie in | S | $(3,8)$ |
Complex Numbers and Quadratic Equations
Solution: