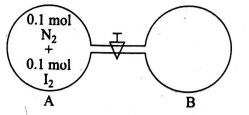
Question

Two vessels of equal volume are connected to each other by a value of negligible volume. One of the containers has $2.8\, g$ of $N _{2} 12.7\, g$ of $I_{2}$ at a temperature $T_{1} .$ The other container is completely evacuated. The container that has $N_{2}$ and $I_{2}$ is heated to temperature $T_{2}$ while the evacuated container is heated $T_{2} / 3 .$ The value is now opened. Calculate the mass of $N _{2}$ in container (B) after a very long time $I_{2}$ sublimes at $T_{2}$. (report your answer in nearest integer form in grams)

Answer 1

Number of moles of $N _{2}$ in vessel
$(A)$ at $T_{1}=\frac{2.8}{2.8}=0.1$
Number of moles of $I_{2}$ in
Vessel (A) at $T_{1}=\frac{12.7}{254}=0.05$

Vessel $(A)$ is heated to $T_{2}$ the evacuated vessel $(B)$ is heated to $T_{2} / 3 .$
On opening stop-cock $I _{2}$ sublimes in $(A)$ and its vapours condense to solid $I_{2}$ in $(B)$. L
et the number of moles of $N _{2}$ moved from $(A)$ to $(B)$ at equilibrium be $x$.
Pressure of $N _{2}$ in $( A )=$ Pressure of $N _{2}$ in $(B)$
$=\frac{(0.1-x) R T_{2}}{V}=\frac{x R T_{2}}{3 V}$
One solving, $x=0.075$
$\therefore $ Mass of $N _{2}$ is vessel $( A )=0.7 \,g$
Mass of $N _{2}$ in vessel $( B )=2.1 \,g$