Question

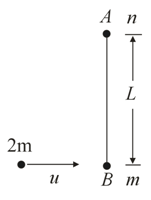
Two small balls $A$ and $B$ , each of mass $m$ , are joined rigidly at the ends of a light rod of length $L$ . They are placed on a frictionless horizontal surface. Another ball of mass $2m$ moving with speed $u$ towards one of the balls and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure. If the coefficient of restitution is $\frac{1}{2}$ , then the angular speed of the rod after the collision will be

• A. $\frac{4}{3}\frac{u}{\ell }$
• B. $\frac{u}{\ell }$
• C. $\frac{2}{3}\frac{u}{\ell }$
• D. None of these

Answer 1

Answer: (B)

If after the collision the velocity of the centre of the rod is $v_{c m}$ towards right, its angular velocity is $\omega $ anti-clockwise and velocity of the ball of mass $2m$ is $v$ . Then,
Applying conservation of momentum,
$2mu=2mv_{c m}+2mv$
$\Rightarrow u=v_{c m}+v\ldots \left(\right.1\left.\right)$
By conservation of angular momentum about the centre of the rod,
$2mu\frac{l}{2}=2m\left(\frac{l}{2}\right)^{2}\omega +2mv\frac{l}{2}$
$\Rightarrow u=\omega \frac{l}{2}+v\ldots \left(\right.2\left.\right)$
And from coefficient restitution,
$e=\frac{1}{2}=\frac{\left(v_{c m} + \omega \frac{l}{2}\right) - v}{u}$
$\Rightarrow u=2v_{c m}+\omega l-2v\ldots \left(\right.3\left.\right)$
After solving these three equations simultaneously we get,
$\omega =\frac{u}{l}$ .