Q.
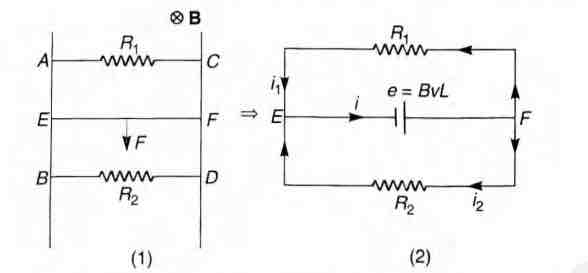
Two parallel vertical metallic rails $AB$ and $CD$ are separated by $1\, m$. They are connected at two ends by resistances $ R_1$ and $R_2$ as shown in figure. A horizontal metallic bar of mass $0.2\, kg$ slides without friction vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of $0.6\, T$ perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in $ R_1$ and $R_2$ are $0.76\, W$ and $1.2\, W$ respectively. Find the terminal velocity of the bar $L$ and the values of $R_1$ and $R_2$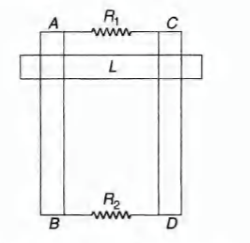
IIT JEEIIT JEE 1994
Solution:
Let the magnetic field be perpendicular to the plane of rails and inwards.
If $v$ be the terminal velocity of the rails, then potential difference across E and F would be $BvL$ with $E$ at lower potential and $F$ at higher potential.
The equivalent circuit is shown in figure (2). In figure (2)
$ i_1 = \frac{ e }{ R_1 } $ ..(i)
$ i_2 = \frac{ e }{ R_2 } $..(ii)
Power dissipated in $R_1$ is $0.76\, W$
Therefore $ei_1 = 0.76\, W $..(iii)
Similarly, $ei_2 = 1.2\, W$ ..(iv)
Now the total current in bar $EF$ is
$ i = i_1 + i_2 $ ( from $E$ to $F$) ...( v)
or $i =3.27\, A$
Multiplying Eq. (v) by e, we get
$ei = ei_1 + ei_2 $
$= (0.76 + 1.2 )$ [From Eqs. (iii) and (iv)]
$= 1.96\, W$
$e = \frac{ 1 .96 }{ i } V = \frac{ 1 . 96 }{ 3 . 2 7 } $
or $e = 0.6\, V$
But since $e = BvL$
$v = \frac{ e }{ BL} = \frac{( 0 . 6 ) }{ ( 0 . 6 ) \, (1 . 0 ) } $
$= 1 . 0\, m/s$.
Hence, terminal velocity of bar is $1.0\, m/s$.
Power in $R_1$ is $0.76\, W$
$\therefore 0.76 = \frac{ e^2 }{ R_1}$
$\Rightarrow \therefore R_1 = \frac{ e^2 }{ 0.76} = \frac{ (0 . 6)^2 }{ 0.76 } $
$= 0 .47\, \Omega \Rightarrow R_1 = 0.47\, \Omega $
Similarly, $R_1 = \frac{ 1}{ 0 . 2} = \frac{ (0 . 6)^2 }{ 1 . 2 } $
$= 0 . 13\, \Omega$
$ R_2 = 0 . 3\, \Omega$.