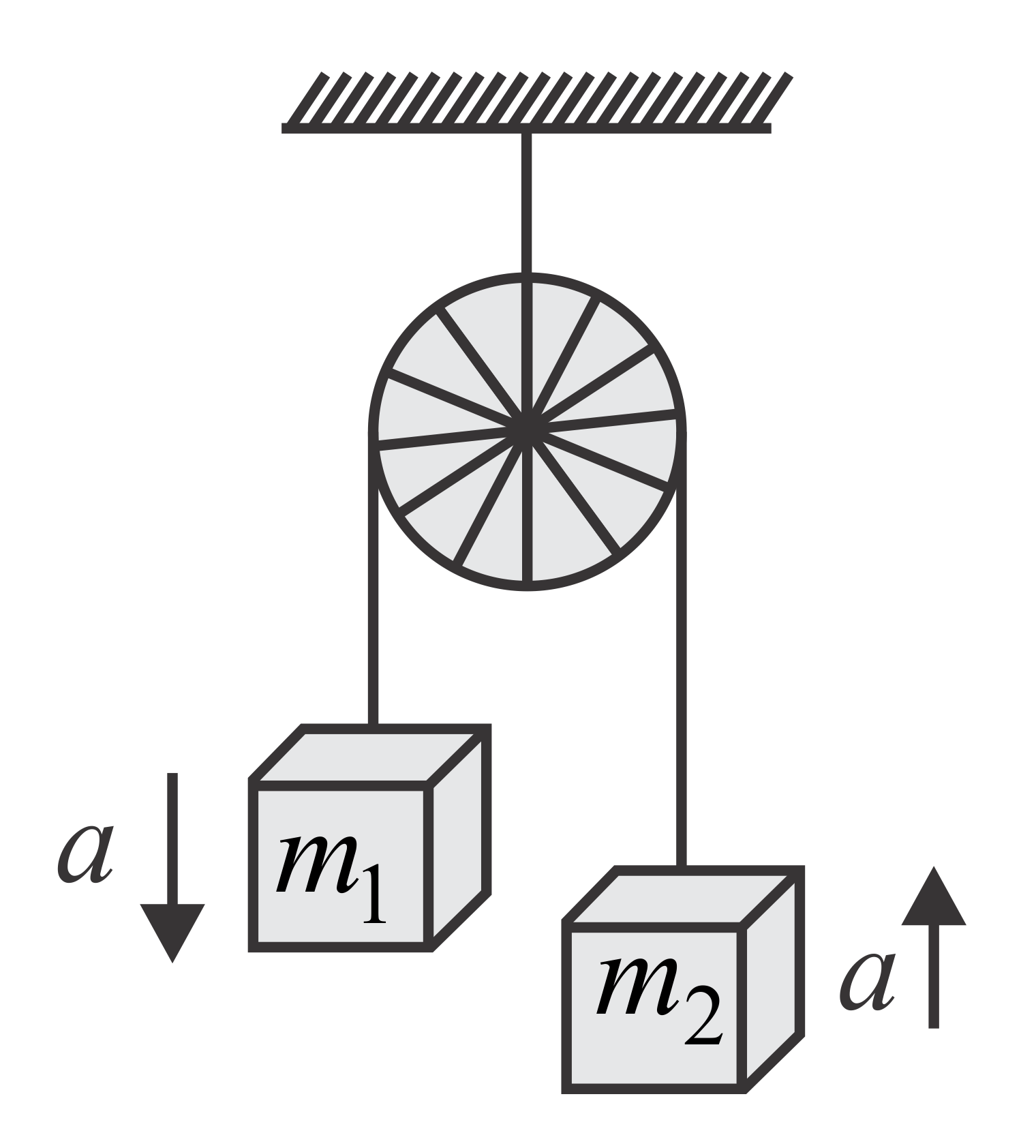
Question

Two masses $m_{1}$ and $m_{2} \, \left(m_{1} > m_{2}\right)$ are connected by a massless flexible and inextensible string passed over a massless and frictionless pulley. The acceleration of the centre of mass is

• A. $\left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)^{2}g$
• B. $\frac{m_{1} - m_{2}}{m_{1} + m_{2}}g$
• C. $\frac{m_{1} + m_{2}}{m_{1} - m_{2}}g$
• D. Zero

Answer 1

Answer: (A)

Acceleration of each mass $=a=\left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)g$
Now acceleration of centre of mass of the system
$A_{c m}=\frac{m_1 \overrightarrow{a_1}+m_1 \overrightarrow{a_2}}{m_1+m_2}$
As both masses move with same acceleration but in opposite direction so $\overrightarrow{a_1}=-\overrightarrow{a_2}=a$ (let)


$\therefore $ $A_{c m}=\frac{m_{1} a - m_{2} a}{m_{1} + m_{2}}$
$=\left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)\times \left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)\times g$
$=\left(\frac{m_{1} - m_{2}}{m_{1} + m_{2}}\right)^{2}\times g$