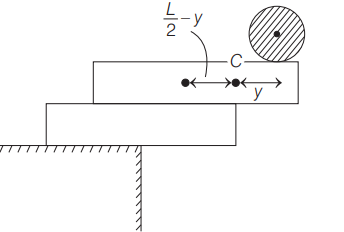
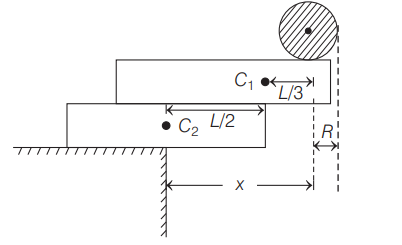
Question

Two identical uniform rectangular blocks (with longest side $L$ ) and a solid sphere of radius $R$ are to be balanced at the edge of a heavy table such that the centre of the sphere remains at the maximum possible horizontal distance from the vertical edge of the table without toppling as indicated in the figure.

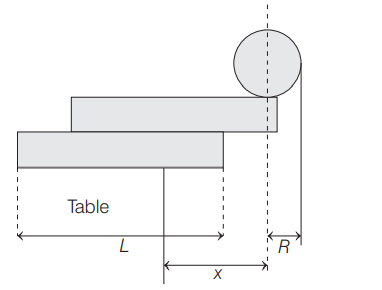
If the mass of each block is $M$ and of the sphere is $M / 2$, then the maximum distance $x$ that can be achieved is

• A. $8 L / 15$
• B. $5 L / 6$
• C. $(3 L / 4+R)$
• D. $(7 L / 15+R)$

Answer 1

Answer: (A)

For system to be in equilibrium without toppling, following conditions must be fulfilled.
(i) Centre of mass $C_{1}$ of sphere and upper block must lie inside the edge of lower block.

Taking origin of axes choosen at $C$, we have
$\frac{M}{2} \times y =M\left(\frac{L}{2}-y\right) $
$\Rightarrow \frac{y}{2}+y =\frac{L}{2} $ or $ y=\frac{L}{3}$
(ii) Centre of mass of both of block and sphere must lie inside the edge of table.

So, again taking centre of mass $C_{2}$ as origin,
$\frac{3 M}{2}\left(x-\frac{L}{3}\right)+M\left(x-\frac{L}{3}-\frac{L}{2}\right)=0$
$\Rightarrow \frac{3 x}{2}-\frac{L}{2}+x-\frac{L}{3}-\frac{L}{2}=0$
$\Rightarrow \frac{5 x}{2}=\frac{4 L}{3}$
$\Rightarrow x=\frac{8 L}{15}$