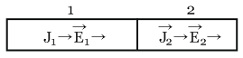
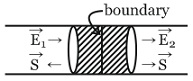
Question

Two cylindrical conductors with equal cross-sections and different resistivities $\rho _{1}$ and $\rho _{2}$ are put end to end. Find the charge at the boundary of the conductors if a current $I$ flows from conductor $1$ to conductor $2$ ._​

• A. $\varepsilon_{0}\left(\rho_{2}-\rho_{1}\right) I$
• B. $\varepsilon_{0}\left(2 \rho_{2}+\rho_{1}\right) I$
• C. $2 \varepsilon_{0}\left(\rho_{1}-\rho_{2}\right) I$
• D. $\varepsilon_{0}\left(\rho_{1}+\rho_{2}\right) I$

Answer 1

Answer: (A)

According to ohm's law, $\overset{ \rightarrow }{\text{E}}=\text{ρ}\overset{ \rightarrow }{\text{J}}$
The problem is solved by the following steps:
Step I: Determine the electric field in both conductors.
The current density in the first conductor is
$J_{1}=\frac{I}{\pi R^{2}}$ (Along the length of the conductor)

Similarly, $J_{2}=\frac{I}{\pi R^{2}}$ (along the length of the conductor)
The electric field inside the first conductor is
$E_{2}=\frac{\rho_{2} I}{\pi R^{2}}$ (along the length of the conductor)
Step II: Consider small cylindrical region near the boundary and apply Gauss's law:
We consider a small cylindrical region at the boundary

The area of the cylindrical region is
$S \, = \, \pi R^{2}$ ​
The net flux through this region is
$\text{ϕ} = \text{ϕ}_{1} + \text{ϕ}_{2} = \overset{ \rightarrow }{\text{E}}_{1} . \overset{ \rightarrow }{\text{S}} + \overset{ \rightarrow }{\text{E}}_{2} \overset{ \rightarrow }{\text{S}}$
$= \, E_{1}S \, cos \, 180^\circ \, + \, E_{2}S \, cos0^\circ = \, - \, E_{1}S \, + \, E_{2}S \, = \, \left(\right.E_{2} \, - \, E_{1}\left.\right) \, S$
According to Gauss's Law,
$ \phi=\frac{ q }{\varepsilon_{0}} $
or $\left(E_{2}-E_{1}\right)=\frac{q}{S \varepsilon_{0}}=\frac{\sigma}{\varepsilon_{0}}$
$\therefore$ The surface charge density at the boundary is
$ \sigma=\left(E_{2}-E_{1}\right) \varepsilon_{0} $
Putting the value of $E_{1}$ and $E_{2}$, we get
$ \therefore \sigma=\left(\rho_{2} j -\rho_{1} j \right) \text { or } \sigma=\left(\rho_{2}-\rho_{1}\right) j $
$ \therefore \sigma=\varepsilon_{0}\left(\rho_{2}-\rho_{1}\right) \frac{ I }{\pi R ^{2}} $
or $\sigma \pi R^{2}=\varepsilon_{0}\left(\rho_{2}-\rho_{1}\right) I$
or $q=\varepsilon_{0}\left(\rho_{2}-\rho_{1}\right) I$
Charge at the boundary $q=\varepsilon_{0}\left(\rho_{2}-\rho_{1}\right) I$