Q.
The wave function, $\psi_{ n , l, m _{\ell}}$ is a mathematical function whose value depends upon spherical polar coordinates ($r, \theta, \phi$ ) of the electron and characterized by the quantum numbers $n , \ell$ and $m _{l} .$ Here $r$ is distance from nucleus, $\theta$ is colatitude and $\phi$ is azimuth. In the mathematical functions given in the Table, $Z$ is atomic number and $a_{0}$ is Bohr radius.
Column 1
Column 2
Column 3
(I) 1s orbital
(i) $\psi_{n, l, m_{l}} \propto\left(\frac{Z}{a_{e}}\right)^{\frac{3}{2}} e^{-\left(\frac{z}{a_{0}}\right)}$
(p) 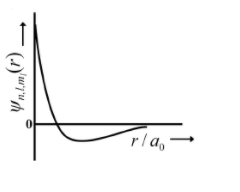
(II) 2s orbital
(ii) one radial node
(Q) Probability density at nucleus $\propto \frac{1}{a^{3}_{0}}$
(III) $2p_{z}$ orbital
(iii) $\psi_{n, l, m_{l}} \propto\left(\frac{Z}{a_{o}}\right)^{\frac{5}{2}} r e^{-\left(\frac{z}{2 a_{0}}\right)} \cos \theta$
(R) Probability density is maximum at nucleus
(IV) $3d^2_z$ Orbital
(iv) xy-plane is a nodal plane
(S) Energy needed to excite electron from $n=2$ state to $n=
4 $ state is $\frac{27}{32}$ times the energy needed to excite electron from $n=2$ state to $n=6$ state
For the given orbital in Column 1, the only CORRECT combination for any hydrogen like species is
| Column 1 | Column 2 | Column 3 |
|---|---|---|
| (I) 1s orbital | (i) $\psi_{n, l, m_{l}} \propto\left(\frac{Z}{a_{e}}\right)^{\frac{3}{2}} e^{-\left(\frac{z}{a_{0}}\right)}$ | (p)  |
| (II) 2s orbital | (ii) one radial node | (Q) Probability density at nucleus $\propto \frac{1}{a^{3}_{0}}$ |
| (III) $2p_{z}$ orbital | (iii) $\psi_{n, l, m_{l}} \propto\left(\frac{Z}{a_{o}}\right)^{\frac{5}{2}} r e^{-\left(\frac{z}{2 a_{0}}\right)} \cos \theta$ | (R) Probability density is maximum at nucleus |
| (IV) $3d^2_z$ Orbital | (iv) xy-plane is a nodal plane | (S) Energy needed to excite electron from $n=2$ state to $n= 4 $ state is $\frac{27}{32}$ times the energy needed to excite electron from $n=2$ state to $n=6$ state |
Solution:
