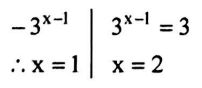Question

The values of $x$, for which the $6^{\text {th }}$ term in the expansion of $\left(2^{\log _{2} \sqrt{\left(9^{x-1}+7\right)}}+\frac{1}{2^{(1 / 5) \log _{2}\left(3^{x-1}+1\right)}}\right)^{7}$ is $84$ are $x_{1}\,\, \&\,\, x_{2}$ then find value of $x_{1}+x_{2}$.

Answer 1

$\left[2^{\log _{2} \sqrt{\left(9^{x-1}+7\right)}}+\frac{1}{2^{(1 / 5) \log _{2}\left(3^{x-1}+1\right)}}\right]^{7}$
$=\left[\sqrt{9^{x-1}+7}+\frac{1}{\left(3^{x-1}+1\right)^{1 / 5}}\right]^{7}$
Here
$T _{6}=84$
$\Rightarrow 7 C_{5} \cdot\left(\sqrt{9^{x-1}+7}\right)^{2} \cdot\left(\frac{1}{\left(3^{x-1}+1\right)^{1 / 5}}\right)^{5}=84$
$\Rightarrow \frac{21 \cdot\left(9^{x-1}+7\right)}{\left(3^{x-1}+1\right)}=84$
$\Rightarrow 9^{x-1}+7=4\left(3^{x-1}+1\right)$
Put $3^{x-1}=t$
$\Rightarrow t^{2}+7=4 t+4$
$\Rightarrow t^{2}-4 t+3=0$
$\Rightarrow t=1$ or $t=3$