1. Tardigrade
  2. Question
  3. Mathematics
  4. The total number of local maxima and local minima of the function f(x)=((2-x)/π) cos (π x+3 π)+(1/π2) sin (π x+3 π), where 0 < x < 4 is equal to

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

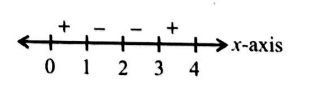
Q. The total number of local maxima and local minima of the function $f(x)=\frac{(2-x)}{\pi} \cos (\pi x+3 \pi)+\frac{1}{\pi^{2}} \sin (\pi x+3 \pi)$, where $0 < x < 4$ is equal to

Application of Derivatives

Solution:

$f'(x)=(2-x) \sin (\pi x)$
image
$\therefore $ Local maximum at $x=1$ and local minimum at $x=3$.