Question

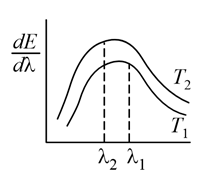
The spectral emissive power $\text{E}_{\lambda }$ for a body at temperature $T_{1}$ is plotted against the wavelength (see figure) and area under the curve is found to be $A$ . At a different temperature $T_{2}$ the area is found to be $9\,A$ . Then $\lambda _{1} / \lambda _{2} =$

• A. $3\,$
• B. $\frac{1}{3}$
• C. $\frac{1}{\sqrt{3}}$
• D. $\sqrt{3}$

Answer 1

Answer: (D)

$\frac{E_1}{E_2}=\frac{1}{9}=\frac{T_1}{T_2}$
$\lambda_1 T_1=\lambda_2 T_2 \Rightarrow \frac{T_1}{T_2}=\frac{\lambda_2}{\lambda_1}$
$\frac{1}{9}=\frac{\lambda_2}{\lambda_1} \Rightarrow \frac{\lambda_2}{\lambda_1}=\frac{1}{\sqrt{3}}$
$\frac{\lambda_1}{\lambda_2}=\sqrt{3}$