Question

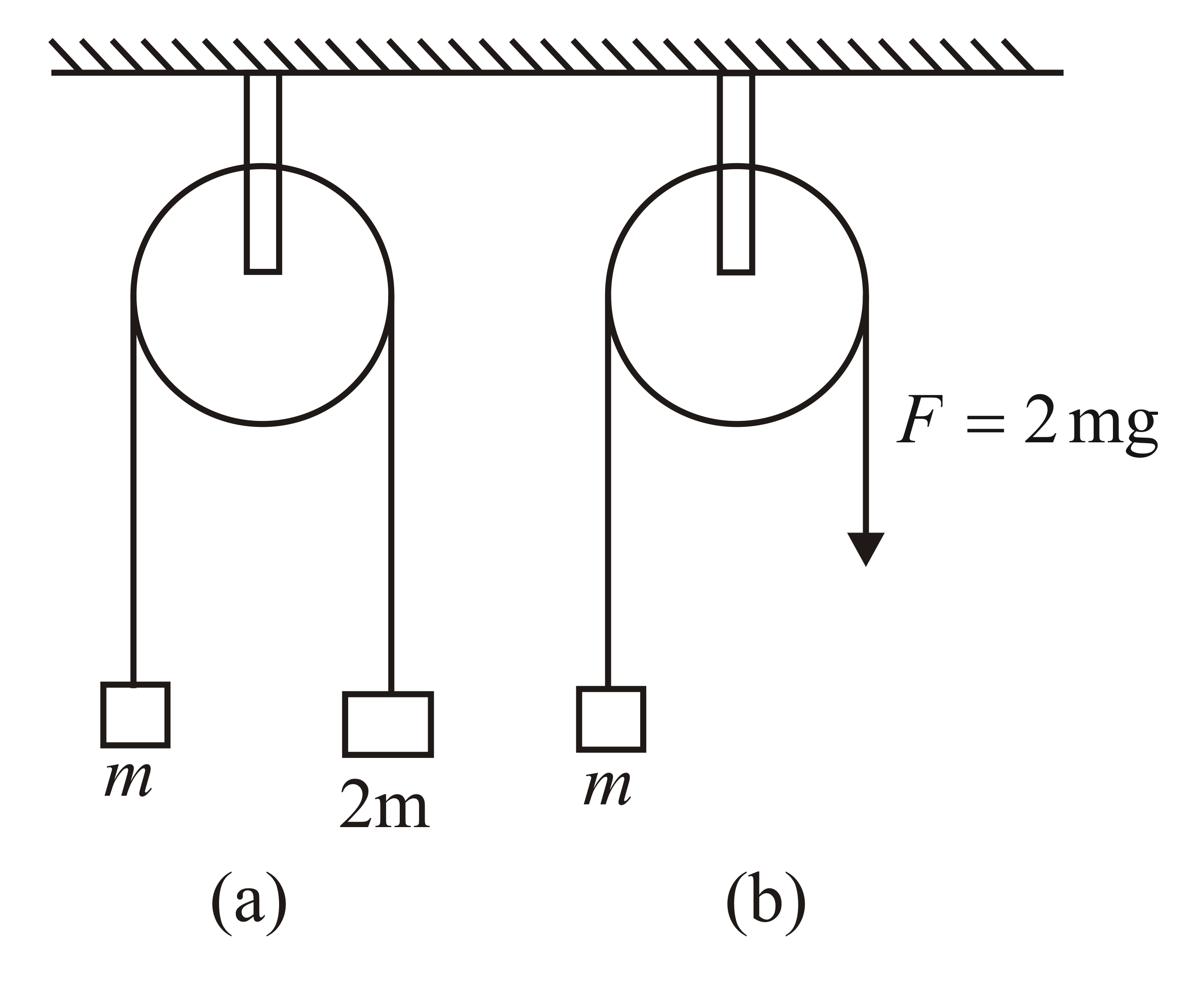
The pulley arrangements shown in the figure are identical, the mass of the rope being negligible. In case $\left(\right.a\left.\right)$ mass $m$ is lifted by attaching a mass of $2m$ to the other end of the rope. In case $\left(\right.b\left.\right)$ the mass $m$ is lifted by pulling the other end of the rope with a constant downward force $F=2mg$ , where $g$ is the acceleration due to gravity. The acceleration of mass $m$ in case $\left(\right.a\left.\right)$ is

• A. zero
• B. more than that in case $\left(\right.b\left.\right)$
• C. Less than that in case $\left(\right.b\left.\right)$
• D. Equal to that in case $\left(\right.b\left.\right)$

Answer 1

Answer: (C)

Let's consider, the acceleration of the blocks in case $\left(a\right)$ and in case $\left(b\right)$ is $a_{1}$ and $a_{2}$ respectively.
In case $\left(a\right)$ ,
Let's assume the Tension force in the string as $T_{1}$ as shown.

From the free body diagram,
$2mg-T_{1}=2ma_{1}$ and
$T_{1}-mg=ma_{1}$
From the above two equations,
$2mg-\left(m g + m a_{1}\right)=2ma_{1}$ ,
$\Rightarrow mg=3ma_{1}$
$\Rightarrow a_{1}=\frac{g}{3}$ .
In case $\left(b\right)$ ,
The Tension in the string, $T_{2}=F=2mg$

Thus, from the free body diagram,
$T_{2}-mg=ma_{2}$
$\Rightarrow 2mg-mg=ma_{2}$
$\Rightarrow a_{2}=g$ .
Therefore, the acceleration in case $\left(a\right)$ is less than that in case $\left(b\right)$ .