Q.
The $P-V$ diagram shown below indicates two paths along which a sample of gas can be taken from state $A$ to state $B$. The energy equal to $5 PV$ in the form of heat is required to be transferred if the Path $-1$ is chosen. How much energy in the form of heat should be transferred if Path-$2$ is chosen?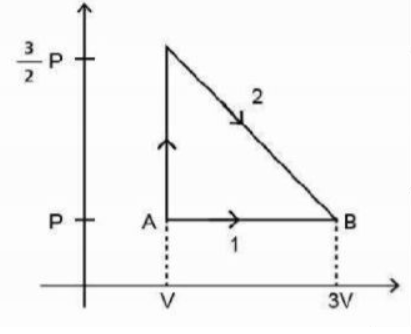
TS EAMCET 2020
Solution:
