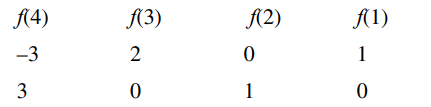Question

The number of functions
$f:\{1,2,3,4\} \rightarrow\{ a \in: Z|a| \leq 8\}$
satisfying $f(n)+\frac{1}{n} f( n +1)=1, \forall n \in\{1,2,3\}$ is

• A. 2
• B. 1
• C. 4
• D. 3

Answer 1

Answer: (A)

$f:\{1,2,3,4\} \rightarrow\{ a \in Z :| a | \leq 8\} $
$ f( n )+\frac{1}{ n } f ( n +1)=1, \forall n \in\{1,2,3\}$
$f( n +1)$ must be divisible by $n$
$f(4) \Rightarrow-6,-3,0,3,6$
$ f(3) \Rightarrow-8,-6,-4,-2,0,2,4,6,8 $
$ f(2) \Rightarrow-8, \ldots \ldots \cdots \cdots \cdots, 8 $
$ f(1) \Rightarrow-8, \ldots \ldots \ldots \ldots \ldots .8$
$\frac{f(4)}{3}$ must be odd since $f(3)$ should be even therefore 2 solution possible.