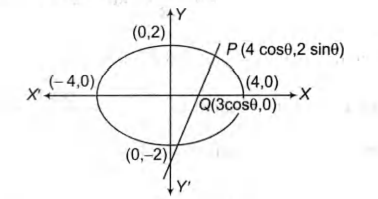
Question

The normal at a point $P$ on the ellipse $ x^2 + 4y^2 = 16 $ meets the $X$-axis at $Q$. If $M$ is the mid-point of the line segment $PQ$, then the locus of $M$ intersects the latus rectum of the given ellipse at the points

• A. $\bigg( \pm \frac{3 \sqrt5}{ 2} , \pm \frac{2}{7} \bigg)$
• B. $\bigg( \pm \frac{3 \sqrt5}{ 2} , \pm \frac{ \sqrt19}{4} \bigg)$
• C. $\bigg( \pm 2\sqrt 3 , \pm \frac{1}{7} \bigg)$
• D. $\bigg( \pm 2\sqrt 3 , \pm \frac{4 \sqrt3}{7} \bigg)$

Answer 1

Answer: (C)

Given, $\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$
Here,
$a=4, b=2$
Equation of normal
$4 x \sec \theta-2 y \operatorname{cosec} \theta=12 $
$M\left(\frac{7 \cos \theta}{2}, \sin \theta\right)=(h, k)$ [say]
$\therefore h=\frac{7 \cos \theta}{2} \Rightarrow=\frac{2 h}{7}=\cos \theta ....$ (i)
and $k=\sin \theta ....$ (ii)
On squaring and adding Eqs. (i) and (ii), we get
$\frac{4 h^{2}}{49}+k^{2}=1 \left[\because \cos ^{2} \theta+\sin ^{2} \theta=1\right]$
Hence, locus is $\frac{4 x^{2}}{49}+y^{2}=1$ .. (iii)

For given ellipse, $e^{2}=1-\frac{4}{16}=\frac{3}{4}$
$\therefore e=\frac{\sqrt{3}}{2}$
$\therefore x=\pm 4 \times \frac{\sqrt{3}}{2}=\pm 2 \sqrt{3} [\because x=\pm a e] \ldots$ (iv)
On solving Eqs. (iii) and (iv), we get
$\frac{4}{49} \times 12+y^{2} =1$
$ \Rightarrow y^{2}=1-\frac{48}{49}=\frac{1}{49} $
$y =\pm \frac{1}{7}$
$\therefore$ Required points $\left(\pm 2 \sqrt{3}, \pm \frac{1}{7}\right)$.