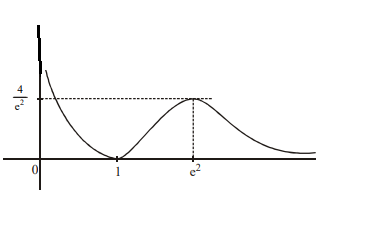
Q. The maximum value of the function $f ( x )=\frac{\ln ^2 x }{ x }$ in $\left[\frac{1}{2}, 10\right]$ is
Application of Derivatives
Solution:

$ f ^{\prime}( x )=\frac{ x 2 \ln x \cdot \frac{1}{ x }-\ln ^2 x }{ x ^2}$
$f ^{\prime}( x )=\frac{\ln x }{ x ^2}(2-\ln x )$
$f(1)=0$ (local minima)
$f \left( e ^2\right)=\frac{4}{ e ^2} \text { (local maxima) } $
$\therefore \text { Maximum occurs at } x =\frac{1}{2}$
$f \left(\frac{1}{2}\right)=2 \ln ^2 2 $