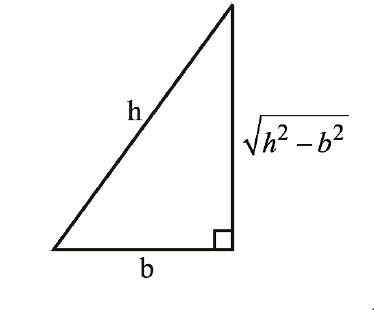Q. The maximum area of a right angled triangle with hypotenuse $h$ is :
Solution:
Let base $= b$
Altitude (or perpendicular) $p \rightarrow \left(q\,\rightarrow \,p\right) $$=\sqrt{h^{2}-b^{2}}$
Area, $A=\frac{1}{2}\times base \times$ altitude
$=\frac{1}{2}\times b\times\sqrt{h^{2}-b^{2}}$
$\Rightarrow \frac{dA}{db}=\frac{1}{2}\left[\sqrt{h^{2}-b^{2}}+b. \frac{-2b}{2\sqrt{h^{2}-b^{2}}}\right]$
$=\frac{1}{2}\left[\frac{h^{2}-2b^{2}}{\sqrt{h^{2}-b^{2}}}\right]$
Put $\frac{dA}{db}=0, \Rightarrow b=\frac{h}{\sqrt{2}}$
Maximum area $=\frac{1}{2}\times\frac{h}{\sqrt{2}}\times\sqrt{h^{2}-\frac{h^{2}}{2}=\frac{h^{2}}{4}}$