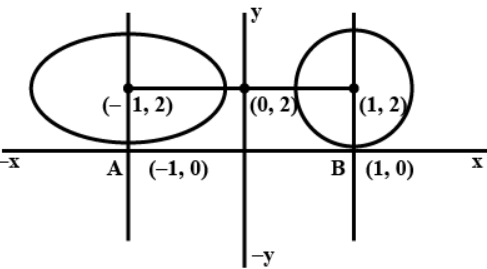
Q. The length of the common chord of the ellipse $\frac{(x+1)^{2}}{9}+\frac{(y-2)^{2}}{4}=1$ and the circle $x-1^{2}+y-2^{2}=1$ is
BITSATBITSAT 2007
Solution:
Given : ellipse equation : $\div(x+1)^{2} 9+\div(y-2)^{2} 4=1$
Circle equation : $(x-1)^{2}+(y-2)^{2}=1$
$\therefore $ center of ellipse $=(-1,2)$
$a =3, b =2$
$\therefore $ length of major axis is $6$
$\therefore $ length of minor is $4$
$\Rightarrow $ center of circle is $(1,2$ with radius $r=1)$
$ \Rightarrow $ so, wecanseeindiagramthatthetwoareasdoesnotintersectortoucheachlengthiso
$\Rightarrow $ Hence, The length of common chord of the ellipse and circle is Zero(o).