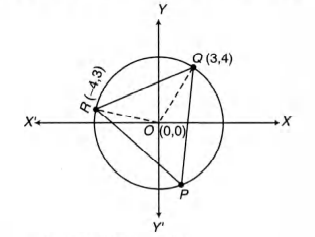
Question

The $\Delta PQR $ is inscribed in the circle $x^2+y^2=25. $ If $Q$ and $R$ have coordinates $(3,4)$ and $(-4, 3)$ respectively, then $\angle QPR $ is equal to

• A. $\pi/2$
  
• B. $\pi/3$
  
• C. $\pi/4$
  
• D. $\pi/6$
  

Answer 1

Answer: (C)

Let $O$ is the point at centre and $P$ is the point at circumference. Therefore, angle $Q O R$ is double the angle $Q P R$. So, it is sufficient to find the angle $Q O R$.

Now, slope of $O Q, m_{1}=4 / 3$,
slope of $O R, m_{2}=-3 / 4$
Here, $ m_{1} m_{2}=-1$
Therefore, $ \angle Q O R=\pi / 2$
which implies that $\angle Q P R=\pi / 4$