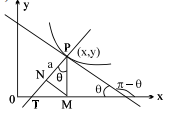
Q. The curve, with the property that the projection of the ordinate on the normal is constant and has a length equal to ' $a$ ', is
Differential Equations
Solution:
$\text { Ordinate }= PM . \text { Let } P \equiv( x , y ) [ T / S ] $
$ \text { Projection of ordinate on normal }= PN$
$PN = PM \cos \theta= a \text { (given) }$
$\therefore \frac{ y }{\sqrt{1+\tan ^2 \theta}}= a \Rightarrow y = a \sqrt{1+\left( y _1\right)^2} $
$\Rightarrow \frac{ dy }{ dx }=\frac{\sqrt{ y ^2- a ^2}}{ a } \Rightarrow \int \frac{ ady }{\sqrt{ y ^2- a ^2}}=\int dx \Rightarrow a \ln \left| y +\sqrt{ y ^2- a ^2}\right|= x + c$