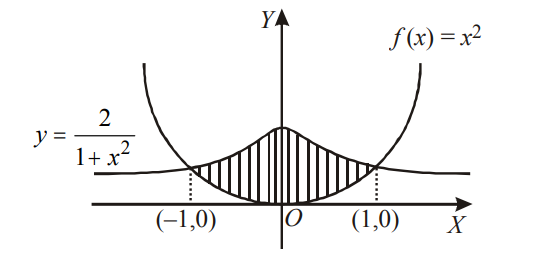
Question

The area bounded by $y=f(x)$ and the curve $y=\frac{2}{1+x^{2}}$ where $f$ is a continuous function satisfying the conditions $f(x) \cdot f(y)=f(x y) . \forall x, y, \in R$ and $f'(1)=2, f(1)=1$ is then

• A. $\left(\pi+\frac{a}{3}\right)$
• B. $\left(\pi-\frac{a}{3}\right)$
• C. $\left(\pi+\frac{2 a}{3}\right)$
• D. None of these

Answer 1

Answer: (B)

$f'(x)=\displaystyle\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$
$\displaystyle\lim _{h \rightarrow 0} \frac{f(x(1+h / x))-f(x)}{h}=\frac{f(x)}{x} \displaystyle\lim _{h \rightarrow 0} \frac{f(1+h / x)-f(1)}{h / x}$
$=\frac{f(x)}{x} \cdot f'(1) $
$\therefore f'(x)=\frac{2 f(x)}{x}$ or $\frac{f'(x)}{f(x)}=\frac{2}{x}$
Integrating both sides, we get, $f(x)=c x^{2}$ Since $f(1)=1, $
$\therefore c=1$

So, $f(x)=x^{2} .$ Now, $\frac{2}{1+x^{2}}=x^{2} $
$\Rightarrow x^{4}+x^{2}-2=0$
$\Rightarrow x^{2}=1 $
$\Rightarrow x=\pm 1$
Required area $=2\left[\int_{0}^{1}\left(\frac{2}{1+x^{2}}-x^{2}\right) d x\right]$
$=2\left[2 \tan ^{-1} x-\frac{x^{3}}{3}\right]_{0}^{1}=2\left[\frac{\pi}{2}-\frac{1}{3}\right]=\left(\pi-\frac{2}{3}\right)$ sq. units.