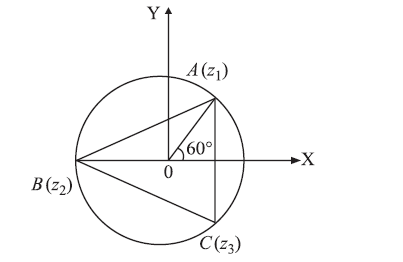
Question

Suppose, $z_{1}, z_{2}, z_{3}$ are the vertices of an equilateral triangle inscribed in the circle $|z|=2$. If $z_{1}=1+i \sqrt{3}$ then $z_{2}$ and $z_{3}$ are equal to

• A. $-2,1-i \sqrt{3}$
• B. $2,1-i \sqrt{3}$
• C. $-2,1+i \sqrt{3}$
• D. None of these

Answer 1

Answer: (A)

$A\left(z_{1}\right), B\left(z_{2}\right), C\left(z_{3}\right)$ lie on $|z|=2$ whose centre is at $O(0,0)$ and radius $2 .$
$z_{1}=1+\sqrt{3} i$ hence $|z|=2$ and $\text{Arg}\left(z_{1}\right)=\frac{\pi}{3}$

In turn $\left|z_{2}\right|=\left|z_{3}\right|=2$ and $\text{Arg}\left(z_{2}\right)=\text{Arg}\left(z_{1}\right)+120^{\circ}=180^{\circ}$
$\therefore z_{2}=-2$
Further, $\text{Arg}\left(z_{3}\right)=\text{Arg}\left(z_{2}\right)+120^{\circ}=300^{\circ}$
Hence, $z_{3}=2\left[\cos \left(2 \pi-\frac{\pi}{3}\right)+i \sin \left(2 \pi-\frac{\pi}{3}\right)\right]$
$=2\left[\cos \frac{\pi}{3}-i \sin \frac{\pi}{3}\right]=2\left(\frac{1}{2}-\frac{i \sqrt{3}}{2}\right)$
$=1-\sqrt{3} i$
Thus, $z_{2}=-2$
and $z_{3}=1-i \sqrt{3}$