Question

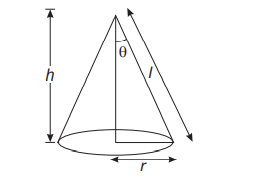
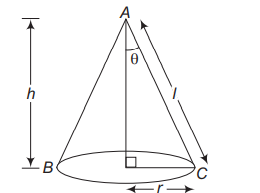
Statement I The semi-vertical angle of the cone of the maximum volume and of given slant height is $\tan ^{-1}\left(\frac{1}{3}\right)$.
Statement II The semi-vertical angle of right circular cone of given surface area and maximum volume is $\sin ^{-1} \sqrt{2}$.

• A. Only statement I is true
• B. Only statement II is true
• C. Both the statements are true
• D. Both the statements are false

Answer 1

Answer: (D)

I. Let $\theta$ be the semi-vertical angle of the cone.
It is clear that $\theta \in\left(0, \frac{\pi}{2}\right)$.
Let $r, h$ and $I$ be the radius, height and the slant height of the cone respectively.
The slant height of the cone is given i.e., consider as constant.
Now, $r=I \sin \theta$ and $h=I \cos \theta$
Let $V$ be the volume of the cone; $V=\frac{\pi}{3} r^2 h$

$\Rightarrow V=\frac{1}{3} \pi\left(I^2 \sin ^2 \theta\right)(l \cos \theta)=\frac{1}{3} \pi l^3 \sin ^2 \theta \cos \theta$
On differentiating w.r.t. $\theta$, we get
$\frac{d V}{d \theta} =\frac{I^3 \pi}{3}\left[\sin ^2 \theta(-\sin \theta)+\cos \theta(2 \sin \theta \cos \theta)\right] $
$ =\frac{I^3 \pi}{3}\left(-\sin ^3 \theta+2 \sin \theta \cos ^2 \theta\right)$
and $\frac{d^2 V}{d \theta^2}=\frac{l^3 \pi}{3}\left(-3 \sin ^2 \theta \cos \theta+2 \cos ^3 \theta -4 \sin ^2 \theta \cos \theta\right)$
$=\frac{l^3 \pi}{3}\left(2 \cos ^3 \theta-7 \sin ^2 \theta \cos \theta\right)$
For maxima put $\frac{d V}{d \theta}=0$
$ \Rightarrow \sin ^3 \theta=2 \sin \theta \cos ^2 \theta$
$ \Rightarrow \tan ^2 \theta=2 $
$ \Rightarrow \tan \theta=\sqrt{2}$
$ \Rightarrow \theta=\tan ^{-1} \sqrt{2} $
Now, when $\theta=\tan ^{-1} \sqrt{2}$, then $\tan ^2 \theta=2$ or $\sin ^2 \theta=2 \cos ^2 \theta$
Then, we have
$\frac{d^2 V}{d \theta^2}=\frac{l^3 \pi}{3}\left(2 \cos ^3 \theta-14 \cos ^3 \theta\right)=-4 \pi l^3 \cos ^3 \theta < 0$ for
$\theta \in\left(0, \frac{\pi}{2}\right)$
$\therefore$ By second derivative test, the volume $V$ is maximum when $\theta=\tan ^{-1} \sqrt{2}$
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is $\tan ^{-1} \sqrt{2}$.
II. With usual notation, given that total surface area
$S=\pi r l+\pi r^2$
$\Rightarrow S=\pi r \sqrt{r^2+h^2}+\pi r^2 \left[\because I=\sqrt{r^2+h^2}\right]$
$\Rightarrow \frac{S}{\pi r}-r=\sqrt{r^2+h^2} \Rightarrow \frac{S^2}{\pi^2 r^2}-\frac{2 S}{\pi}=h^2$
$\Rightarrow h=\sqrt{\frac{S^2}{\pi^2 r^2}-\frac{2 S}{\pi}},\left(\because \frac{S^2}{\pi^2 r^2}>\frac{2 S}{\pi}\right) .....$(i)
and volume $V=\frac{1}{3} \pi r^2 h$
$=\frac{1}{3} \pi r^2 \sqrt{\frac{S^2}{\pi^2 r^2}-\frac{2 S}{\pi}}$
$\Rightarrow V=\frac{r}{3} \sqrt{S^2-2 S \pi r^2}, r^2 < \frac{S}{2 \pi} i \cdot e ., 0 < r < \sqrt{\frac{S}{2 \pi}}$
Since, $V$ is maximum, then $V^2$ is maximum.

Now, $ V^2=\frac{S^2 r^2}{9}-\frac{2 S \pi r^4}{9}, 0 < r < \sqrt{\frac{S}{2 \pi}}$
$\therefore \frac{d}{d r}\left(V^2\right)=\frac{2 r S^2}{9}-\frac{8 S \pi r^3}{9}$
and $\frac{d^2}{d r^2}\left(V^2\right)=\frac{2 S^2}{9}-\frac{24 S \pi r^2}{9}$
For maxima, put $\frac{d}{d r}\left(V^2\right)=0$
$\Rightarrow \frac{2 r S^2}{9}-\frac{8 S \pi r^3}{9}=0$
$ \Rightarrow r^2=\frac{S}{4 \pi} $
$\Rightarrow r=\sqrt{\frac{S}{4 \pi}} $
Here, $\frac{d^2\left(V^2\right)}{d r^2}<0 $ for $ r=\sqrt{\frac{S}{4 \pi}}$
So, $V^2$ and hence, $V$ is maximum, when $r=\sqrt{\frac{S}{4 \pi}}$
From Eq. (i), $h=\sqrt{\frac{S^2}{\pi^2 r^2}-\frac{2 S}{\pi}}=\sqrt{\frac{S^2(4 \pi)}{\pi^2 S}-\frac{2 S}{\pi}}=\sqrt{\frac{2 S}{\pi}}$
If $\theta$ is the semi-vertical angle of the cone when the volume is maximum, then in right triangle $A O C$,
$\sin \theta=\frac{r}{\sqrt{r^2+h^2}}=\frac{\sqrt{\frac{S}{4 \pi}}}{\sqrt{\frac{S}{4 \pi}+\frac{2 S}{\pi}}}=\frac{1}{\sqrt{1+8}}$
i.e.,$\theta = \sin^{-1}(\frac{1}{3})$
So, the both the given statements are false.