Q.
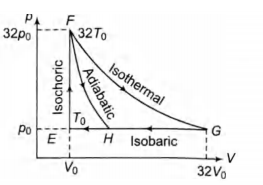
One mole of a monatomic ideal gas is taken along two cyclic processes E $\rightarrow$ F $\rightarrow$ G $\rightarrow$ E and E $\rightarrow$ F $\rightarrow$ H $\rightarrow$ E as shown in the p-V diagram.
The processes involved are purely isochoric, isobaric, isothermal or adiabatic.
Match the paths in List I with the magnitudes of the work done in List II and select the correct answer using the codes given below the lists.

List I
List II
P.
$G \to E$
1.
$160\, p_{0}V_{0}$ In 2
Q.
$G \to H$
2
$36\,P_{0}V_{0}$
R.
$F \to H$
3.
$24\, P_{0}V_{0}$
S.
$F \to G$
4.
$31\, P_{0}V_{0}$
| List I | List II | ||
|---|---|---|---|
| P. | $G \to E$ | 1. | $160\, p_{0}V_{0}$ In 2 |
| Q. | $G \to H$ | 2 | $36\,P_{0}V_{0}$ |
| R. | $F \to H$ | 3. | $24\, P_{0}V_{0}$ |
| S. | $F \to G$ | 4. | $31\, P_{0}V_{0}$ |
Solution:
In F $\rightarrow$ G work done in isothermal process is
$nRT \, ln \bigg(\frac{V_f}{V_i}\bigg)=32p_0V_0 \, ln \bigg(\frac{32V_0}{V_0}\bigg)$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, =32p_0V_0 \, ln 2^5=160p_0v_0 ln 2$
in G $\rightarrow \, \, E,\Delta W=p_0 \Delta v=p_0(31v_0)=31p_0v_0$
in G $\rightarrow$ work done is less than $31p_0v_0 \, i.e., 24 p_0v_0$
in F $\rightarrow$ work done is 36 p$_0V_0$