Question

Match the rate expressions in LIST-I for the decomposition of $X$ with the corresponding profiles provided in LIST-II. $X _{ s }$ and $k$ constants having appropriate units.

LIST I		LIST II
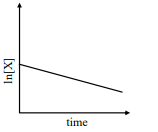
I	$\text { rate }=\frac{ k [ X ]}{ X _{ s }+[ X ]}$ under all possible initial concentration of $X$	i
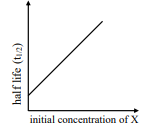
II	$ \text { rate }=\frac{ k [ X ]}{ X _{ s }+[ X ]} $ where initial concentration of $X$ are much less than $X _s$	ii
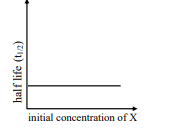
III	$ \text { rate }=\frac{ k [ X ]}{ X _{ s }+[ X ]} $ where initial concentration of $X$ are much higher than $X _{ s }$	iii
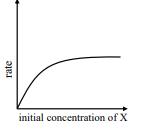
IV	$ \text { rate }=\frac{ k [ X ]^2}{ X _{ s }+[ X ]} $ ,br/>where initial concentration of $X$ is much higher than $X _{ s }$	iv
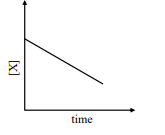
		v

• A. I $\rightarrow$ P; II $\rightarrow$ Q; III $\rightarrow$ S; IV $\rightarrow$ T
• B. $I \rightarrow R$; II $\rightarrow$ S; III $\rightarrow$ S; IV $\rightarrow$ T
• C. I $\rightarrow$ P; II $\rightarrow$ Q; III $\rightarrow$ Q; IV $\rightarrow$ R
• D. $I \rightarrow R$; II $\rightarrow S$; III $\rightarrow$ Q; IV $\rightarrow R$

Answer 1

Answer: (A)

(I)$\text { rate }=\frac{ k [ x ]}{ x _{ s }+[ x ]}=\frac{ k }{\frac{ x _{ s }}{[ x ]}+1}$
$ \text { If }[ x ] \rightarrow \infty \Rightarrow \text { rate } \rightarrow k \Rightarrow \text { order }=0 $
$ \Rightarrow ( I )-( R ),( P )$
(II)$ {[ x ]< < x _{ s } \Rightarrow \text { rate }=\frac{ k [ x ]}{ x _{ s }} \Rightarrow \text { order }=1} $
$ \Rightarrow \text { (II) }-( Q ), \text { (T) }$
(III) $[ x ]>> x _{ s } \Rightarrow$ rate $= k \Rightarrow$ order $=0$
$\Rightarrow ( III )-( P ),( S )$
(IV)$ \text { rate }=\frac{ k [ x ]^2}{ x _{ s }+[ x ]} $
$ {[ x ]>> x _{ s } \Rightarrow \text { rate }= k [ x ] } $
$ \Rightarrow( IV )-( Q ),( T )$