Q.
Match the following continuous series given in Column I with their corresponding mean deviations about mean or median in Column II and choose the correct option from the codes given below.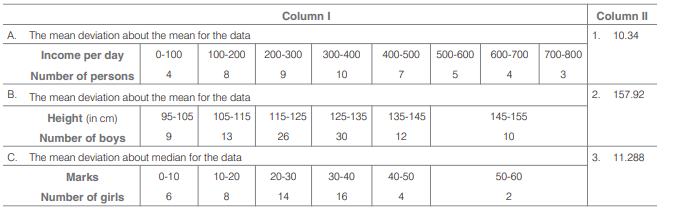
Statistics
Solution:
A .
Class
$f_i$
Mid value $(x_i)$
$d_i = \frac{x_i-A}{h} A = 350, h = 100$
$f_i d_i |$
|x_i - \bar{x}|$
$f_i |x_i - \bar{x}|$
0- 100
4
50
-3
-12
308
1232
100-200
8
150
-2
-16
208
1664
200-300
9
250
-1
-9
108
972
300-400
10
350
0
0
8
80
400-500
7
450
1
7
92
644
500-600
5
550
2
10
192
960
600-700
4
650
3
12
292
1168
700-800
3
750
4
12
392
1176
Total
$\Sigma f_i = 50$
4
7896
Mean $ \bar{x} =A+\frac{\Sigma f d_i}{\Sigma f_i} \times h=350+\frac{4}{50} \times 100=350+8 $
$\bar{x} =358$
Mean deviation about the mean
$=\frac{\Sigma f_i\left|x_i-\bar{x}\right|}{\Sigma f_i}=\frac{7896}{50}=157.92$
Class
$f_i$
Mid value $(x_i)$
$d_i = \frac{x_i-A}{h} A = 350, h = 100$
$f_i d_i |$
|x_i - \bar{x}|$
$f_i |x_i - \bar{x}|$
95- 105
9
100
-3
-27
25.3
227.7
105-115
13
110
-2
-26
15.3
198.9
115-125
26
120
-1
-26
5.3
137.8
125-135
30
130
0
0
4.7
141.0
135-145
12
140
1
12
14.7
176.4
145-155
10
150
2
20
24.7
247.0
Total
100
-47
1128.8
Mean $(\bar{x})=A+\frac{\Sigma f_i d_i}{\Sigma f_i} \times h $
$= 130+\frac{(-47)}{100} \times 10=130-4.7=125.3$
Mean deviation about mean $=\frac{\Sigma f_i\left|x_i-\bar{x}\right|}{\Sigma f_i}=\frac{1128.8}{100} $
$=11.288$
Class
$f_i$
$cf$
Mid value $(x_i)$
$|x_i - M|$
$f_i |x_i - M|$
0 - 10
6
6
5
|5 - 27.86|= 22.86
137.16
10 - 20
8
(14)C
15
|15 - 27.86| = 12.86
102.88
(20-30)
(14)
28
25
|25-27.86| = 2.86
40.04
30 - 40
16
44
35
|35-27.86| = 7.14
114.24
40 - 50
4
48
45
|45 - 27.86| = 17.14
68.56
50 - 60
2
50
55
|55 - 27.86| = 27.14
54.28
Total
$\Sigma f_i = 50$
517.16
Here, $ \frac{N}{2} =\frac{50}{2}=25 $
$ \Rightarrow C =14, f=14, I=20, h=10 $
Median $(M) =I+\frac{\frac{N}{2}-C}{f} \times h $
$ =20+\frac{25-14}{14} \times 10 $
$ =20+\frac{11 \times 10}{14} $
$=20+7.86=27.86$
$ \therefore $ Mean deviation about median $= \frac{\Sigma f_i\left|x_i-M\right|}{\Sigma f_i}$
$=\frac{517.16}{50}=10.34$
| Class | $f_i$ | Mid value $(x_i)$ | $d_i = \frac{x_i-A}{h} A = 350, h = 100$ | $f_i d_i |$ | |x_i - \bar{x}|$ | $f_i |x_i - \bar{x}|$ |
|---|---|---|---|---|---|---|
| 0- 100 | 4 | 50 | -3 | -12 | 308 | 1232 |
| 100-200 | 8 | 150 | -2 | -16 | 208 | 1664 |
| 200-300 | 9 | 250 | -1 | -9 | 108 | 972 |
| 300-400 | 10 | 350 | 0 | 0 | 8 | 80 |
| 400-500 | 7 | 450 | 1 | 7 | 92 | 644 |
| 500-600 | 5 | 550 | 2 | 10 | 192 | 960 |
| 600-700 | 4 | 650 | 3 | 12 | 292 | 1168 |
| 700-800 | 3 | 750 | 4 | 12 | 392 | 1176 |
| Total | $\Sigma f_i = 50$ | 4 | 7896 |
| Class | $f_i$ | Mid value $(x_i)$ | $d_i = \frac{x_i-A}{h} A = 350, h = 100$ | $f_i d_i |$ | |x_i - \bar{x}|$ | $f_i |x_i - \bar{x}|$ |
|---|---|---|---|---|---|---|
| 95- 105 | 9 | 100 | -3 | -27 | 25.3 | 227.7 |
| 105-115 | 13 | 110 | -2 | -26 | 15.3 | 198.9 |
| 115-125 | 26 | 120 | -1 | -26 | 5.3 | 137.8 |
| 125-135 | 30 | 130 | 0 | 0 | 4.7 | 141.0 |
| 135-145 | 12 | 140 | 1 | 12 | 14.7 | 176.4 |
| 145-155 | 10 | 150 | 2 | 20 | 24.7 | 247.0 |
| Total | 100 | -47 | 1128.8 |
| Class | $f_i$ | $cf$ | Mid value $(x_i)$ | $|x_i - M|$ | $f_i |x_i - M|$ |
|---|---|---|---|---|---|
| 0 - 10 | 6 | 6 | 5 | |5 - 27.86|= 22.86 | 137.16 |
| 10 - 20 | 8 | (14)C | 15 | |15 - 27.86| = 12.86 | 102.88 |
| (20-30) | (14) | 28 | 25 | |25-27.86| = 2.86 | 40.04 |
| 30 - 40 | 16 | 44 | 35 | |35-27.86| = 7.14 | 114.24 |
| 40 - 50 | 4 | 48 | 45 | |45 - 27.86| = 17.14 | 68.56 |
| 50 - 60 | 2 | 50 | 55 | |55 - 27.86| = 27.14 | 54.28 |
| Total | $\Sigma f_i = 50$ | 517.16 |