1. Tardigrade
  2. Question
  3. Mathematics
  4. Lot of be any function continuous on [a, b ] and twice differentiable on (a, b). If for all x ϵ (a, b ) , f'( x ) > 0 and f'' ( x ) < 0, then for any c ϵ (a, b), (f(c) - f(a)/f(b)-f(c)) is greater than :

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. Lot of be any function continuous on [$a, b$ ] and twice differentiable on (a, b). If for all x $\epsilon$ ($a, b $ ) , $f'( x ) > 0\, and f'' ( x ) < 0$, then for any $c \epsilon$ ($a, b$), $\frac{f\left(c\right) - f\left(a\right)}{f\left(b\right)-f\left(c\right)}$ is greater than :

JEE MainJEE Main 2020Application of Derivatives

Solution:

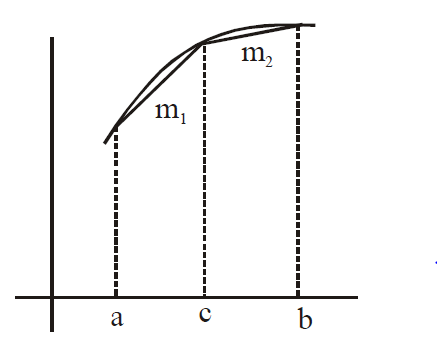
it is clear from graph that $m_1 > m_2$
$\Rightarrow \frac{f \left(c\right)-f \left(a\right)}{c-a} > \frac{f \left(b\right)-f \left(c\right)}{b-c}$
$\frac{ f \left(c\right)-f \left(a\right)}{f \left(b\right)-f \left(c\right)} > \frac{c-a}{b-c}$

Solution Image