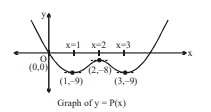
Question

Let $P(x)$ be a polynomial of degree 4 having a relative maximum at $x=2$ and $\underset{x \rightarrow 0}{\text{Lim}} \left(3-\frac{P(x)}{x}\right)=27$. Also $P (1)=-9$ and $P ^{\prime \prime}( x )$ has a local minimum at $x =2$.
The value of definite integral $\int_0^1(P(-x)-P(x)) d x$ equals

• A. 12
• B. 16
• C. 28
• D. 24

Answer 1

Answer: (C)

We have
$\underset {x \rightarrow 0}{\text{Lim}}\left(3-\frac{P(x)}{x}\right)=27 \Rightarrow \underset {x \rightarrow 0}{\text{Lim}} \frac{P(x)}{x}=-24$
$\therefore$ Let $P ( x )= ax ^4+ bx ^3+ cx ^2-24 x$....(1)
Now, $P(1)=-9 \Rightarrow a+b+c=15$....(2)
Also, $ P^{\prime}(2)=0 \Rightarrow 8 a+3 b+c=6$....(3)
and $ P^{\prime \prime \prime}(2)=0 \Rightarrow b=-8 a$....(4)
$\therefore$ On solving (2), (3), (4), we get
$a =1, b =-8, c =22$
Hence, $P(x)=x^4-8 x^3+22 x^2-24 x$....(5)

$\therefore P^{\prime}(x)=4 x^3-24 x^2+44 x-24=4\left(x^3-6 x^2+11 x-6\right)=4(x-1)(x-2)(x-3) $
$\Rightarrow P^{\prime \prime}(x)=4\left(3 x^2-12 x+11\right)$
Clearly, $P ^{\prime \prime}( x )>0 \forall x \in[3,4]$ (As $P ^{\prime}( x )$ is increasing function on $[3,4]$ )
Consider,
$\int\limits_0^1(P(-x)-P(x)) d x=\int\limits_0^1\left(\left(x^4+8 x^3+22 x^2+24 x\right)-\left(x^4-8 x^3+22 x^2-24 x\right)\right) d x $
$=\int\limits_0^1\left(16 x^3+48 x\right) d x=16 \int\limits_0^1\left(x^3+3 x\right) d x=16\left(\frac{x^4}{4}+\frac{3 x^2}{2}\right)_0^1=16\left(\frac{1}{4}+\frac{3}{2}\right)=4+24=28 .$