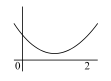
Question

Let $f( x )= x ^2+ ax + b$. If the maximum and the minimum values of $f( x )$ are 3 and 2 respectively for $0 \leq x \leq 2$, then the possible ordered pair(s) of (a, b) is/are

• A. $(-2,3)$
• B. $(-3 / 2,2)$
• C. $(-5 / 2,3)$
• D. $(-5 / 2,2)$

Answer 1

Answer: (A)

$f ( x )= x ^2+ ax + b$
vertex of $f(x)$ is at $-\frac{a}{2}$
f $0 \leq-\frac{a}{2} \leq 2$
i.e. $0 \leq- a \leq 4 ; -4 \leq a \leq 0$

$f ( x )]_{\min }= f \left(-\frac{ a }{2}\right)=\frac{ a ^2}{4}-\frac{ a ^2}{2}+ b = b -\frac{ a ^2}{4}=2$ ....(1)
and $f(x)]_{\max }=f(0)$ or $f(2)$
but $f(0)=b$ and $f(2)=4+2 a+b$
let $b =3$;
from(1) $ 3-\frac{ a ^2}{4}=2 ; \frac{ a ^2}{4}=1 \Rightarrow a =2$ or -2
but $a =2$ is rejected hence $a =-2$
$\therefore (-2,3)$ Ans. $\Rightarrow$ (A)
if $f (2)$ is maximum
$4+2 x + b =3 \Rightarrow 2 a + b =-1$
(2) - (1) gives, $2 a+\frac{a^2}{4}=-3 \Rightarrow a^2+8 a+12=0 p(a+6)(a+2)=0$ $a=-2$ or $a=-6$ (rejected)
for vertex $<0$ or vertex $>2$ their are no accepted ordered pairs. Hence only $( A )$ is correct